class: center, middle, inverse, title-slide .title[ # 财务管理理论与实务 ] .subtitle[ ## Regression ] .author[ ### 唐润宇 ] .date[ ### 2023-10-12 ] --- # 回归 Regression is a method for studying the relationship between a response variable (因变量) Y and a covariate(自变量) X. 为什么叫回归？ 高尔顿：最著名的发现之一是他发现了父亲的身高和儿子的身高之间存在着某种给定的关系，他通过进一步的研究发现了： > 子辈的平均身高是其父辈平均身高以及他们所处族群平均身高的加权平均和。 > 哪怕单看一组父亲和孩子的身高，两个人的身高可能差异很大，但是从整个人群上来看，父亲和孩子的身高分布应该是很相近的。 回归模型的作用: - 一种强有力的基于数据的预测模型工具 - 建立反应一个变量的变化与其他变量变化的公式。 --- ## 监督学习 在机器学习的场景里面， 回归是一种监督学习的工具。 （对比于上节课的聚类：无监督学习） 除了回归这种方法，其他的常见监督学习方法： - CART (Classification And Regression Tree) 树模型 - Kernel Smoothing method - SVM 支持向量机 - Nearest-Neighbors 近邻法 - ... --- ## 线性回归 - 因变量: 想要预测和分析的变量，通常用 `\(Y\)`表示。 - 自变量: 解释因变量的变量，通常用 `\(x_1, x_2, …, x_p\)` 表示。 - 线性回归: `$$𝑌=𝛽_0+𝛽_1 𝑥_1+ …+𝛽_p 𝑥_p+𝜖$$` - 一元线性回归 $$ Y = \beta_0 + \beta_1 x + \epsilon $$ --- ## 一元线性回归 - 数据: `\((𝑥_𝑖, 𝑦_𝑖 ), \quad 𝑖=1,…,𝑛\)`. - 我们希望找到一根直线，“最好”地拟合数据 - 找直线： →估计 `\(𝛽_0, \beta_1\)` - "最好"： `\(𝑦_𝑖\)`与 `\(\hat{y}_i\)` 足够接近 → 最小二乘法！ $$ `\begin{align*} \min_{\beta_0, \beta_1} Q(\beta_0, \beta_1) &= \min_{\beta_0, \beta_1} \sum_{i=0}^n (y_i - \hat{y}_i)^2\\ &= \min_{\beta_0, \beta_1} \sum_{i=0}^n \left(y_i - (\beta_0 + \beta_1 x_i) \right)^2 \end{align*}` $$ --- ## 最小二乘法 .pull-left[  ] .pull-right[ 高斯使用的最小二乘法的方法发表于1809年他的著作《天体运动论》中，而法国科学家勒让德于1806年独立发现“最小二乘法”，但因不为世人所知而默默无闻。两人曾为谁最早创立最小二乘法原理发生争执。 ] --- ## 最小二乘法 .pull-left[ 误差平方和 `\(Q(\beta_0, \beta_1)\)` 是关于 `\(𝛽_0, 𝛽_1\)` 的一个联合凸函数(convex function) 求导使用FOC (first-order condition) $$ `\begin{align*} & \left\{ \begin{aligned} \frac{\partial Q}{\partial \beta_0} = 0 \\ \frac{\partial Q}{\partial \beta_1} = 0 \\ \end{aligned} \right. \\ \Rightarrow & \left\{ \begin{aligned} &\hat{\beta}_1 = \frac{\sum_{i=1}^n (x_i - \bar{x}) (y_i - \bar{y})}{\sum_{i=1}^n (x_i - \bar{x})^2} \\ &\hat{\beta}_0 = \bar{y} - \hat{\beta}_1 \bar{x} \\ \end{aligned} \right. \end{align*}` $$ Note. 回归的直线会穿过样本重心 `\((\bar{x}, \bar{y})\)`. ] .pull-right[  ] --- ## 最小二乘法的性质 - **线性性**: `\(\hat{\beta}_0\)` 和 `\(\hat{\beta}_1\)` 都是 `\(𝑦_𝑖\)` 的线性函数。 - **无偏性**: `$$E[\hat{\beta}_1 ]=\beta_1, \quad E[\hat{\beta}_0 ]=\beta_0.$$` 这里需要假设 `\(𝑦_𝑖=𝛽_0+𝛽_1 𝑥_𝑖+𝜖_𝑖\)` for all `\(i=1,2,…,n\)`, 其中 `\(𝐸[\epsilon_i]=0\)` for all `\(i=1,2,…,n\)`. - **回归参数估计值的方差**: $$ `\begin{align*} &var(\hat{\beta}_1) =\frac{\sigma^2}{\sum_{i=1}^n (x_i -\bar{x})^2} \\ &var(\hat{\beta}_1) = \left(\frac{1}{n} + \frac{\bar{x}^2}{\sum_{i=1}^n (x_i -\bar{x})^2} \right) \sigma^2 \end{align*}` $$ 需要假设 `\(\epsilon_i \sim N(0, \sigma^2 )\)` 独立同分布 i.i.d --- ## 回归方程 下面的论述是否正确？ - 对于任意两组数据，我们都可以跑线性回归估计出对应的 `\(\hat{\beta}_0\)` 和 `\(\hat\beta_1\)`. -- <!-- --> <!-- --> 我们可以通过系数大小判断线性相关程度吗？ --- ## R square  .center[SST = SSR + SSE] --- ## R square $$ R^2=1− \frac{\sum(y_i - \hat{y}_i)^2}{\sum(y_i - \bar{y})^2} =\frac{\text{SSR}}{\text{SST}} $$ &nbsp; `\(R^2\)`是由自变量 `\(x_1, x_2,...,x_p\)`的线性回归等式解释的因变量 `\(Y\)`的观测值变化占总变化的比例。 - 如果在总的离差平方和中回归平方和所占的比重越大，则线性回归效果就越好,这说明回归直线与样本观测值拟合优度就越好；如果残差平方和所占的比重大，则回归直线与样本观测值拟合得不理想。 - `\(R^2\)`的数值总是在0到1之间，如果数值越高，回归模型的拟合效果越好。 --- ## R square `\(R^2\)` 总在0-1之间，但是可接受程度在不同的场合下是不同的 > 宏观经济模型（比如GNP）中, `\(R^2 = 0.35\)`是可以接受的; > 在成本模型中 `\(R^2\)`=0.75也是难以接受的 - 相关关系≠因果关系！ > 公鸡打鸣-> 太阳升起、 打雷->闪电 - 相关但是不是原因！ > 冬天的羽绒服销量高 and 冬天的天然气用量高 --- ## 线性回归 in R ```r library(tidyverse) setwd("~/XJTU/课程/财务管理理论与实务/Codes") data <- read_csv("BYD_data.csv") data |> ggplot(mapping = aes(x = RDCost, y = OpeRev)) + geom_point()+ geom_smooth() ``` 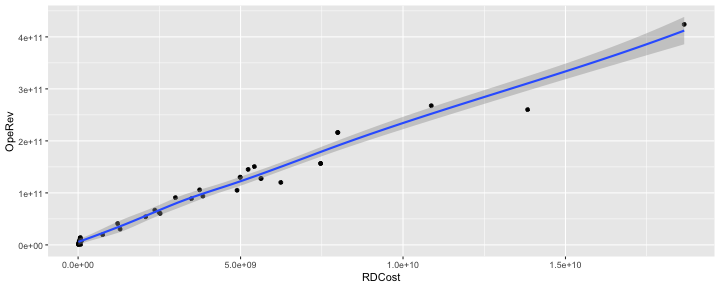<!-- --> --- ## 线性回归 in R ```r fit <- lm(OpeRev~RDCost, data) summary(fit) ``` ``` ## ## Call: ## lm(formula = OpeRev ~ RDCost, data = data) ## ## Residuals: ## Min 1Q Median 3Q Max ## -5.366e+10 -5.273e+09 -1.259e+09 3.992e+09 3.147e+10 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 8.126e+09 2.528e+09 3.214 0.00239 ** ## RDCost 2.209e+01 5.045e-01 43.793 < 2e-16 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 1.397e+10 on 46 degrees of freedom ## (2 observations deleted due to missingness) ## Multiple R-squared: 0.9766, Adjusted R-squared: 0.9761 ## F-statistic: 1918 on 1 and 46 DF, p-value: < 2.2e-16 ``` --- ## 回归方程的显著性检验 - **假设检验**：原假设 `\(H_0: \beta_1 = 0\)` v.s. 备择假设 `\(H_1: \beta_1 \neq 0\)`. - 回归系数的显著性检验就是要检验因变量 y 对自变量 x 的影响程度是否显著。如果不显著，则因变量 y 与自变量 x 之间并没有真正的线性关系，也就是说自变量 x 的变化对因变量 y 并没有影响。 <img src="Figs/hypoTest.jpg" width="569" style="display: block; margin: auto;" /> --- ## 假设检验 **大前提**: `\(\epsilon_i \sim N(0, \sigma^2)\)` 且i.i.d. , 此时 `$$\hat{\beta}_1 \sim N \left(\beta_1, \frac{\sigma^2}{\sum_{i=1}^n (x_i - \bar{x})^2}\right).$$` - t 检验 $$ `\begin{align*} t=\frac{\hat{\beta}_1 \sqrt{\sum_{i=1}^n (x_i - \bar{x})^2} }{\hat{\sigma}} \sim t(n-2). \end{align*}` $$ - F 检验 `$$F=\frac{\text{SSR}/1}{\text{SSE}/(n-2)} \sim F (1, n-2).$$` --- ## P value “离谱”的概率：如果原假设成立，出现比当前状况更离谱状况的概率。 - 较小的p-value表示原假设比较“离谱”，因此更支持备择假设 通常我们使用α = 0.05作为基准. > p-value < 0.05 is “small” = “statistically significant”. > p-value > 0.05 is “large” = “not statistically significant”. - p-value = 0.049 versus p-value = 0.051? > Charles Geyer: “The traditional 0.05 dividing line has nothing to recommend it other than that it is a round number. It is a round number because humans have five fingers.” - Many advocate abandoning the 0.05 cutoff point. --- ## 残差分析 ```r plot(fit) ``` 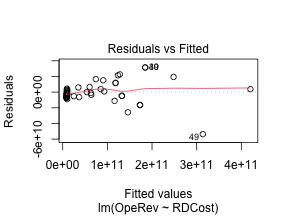<!-- -->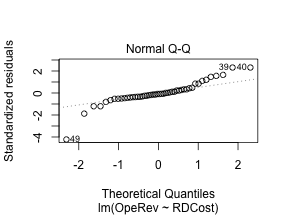<!-- -->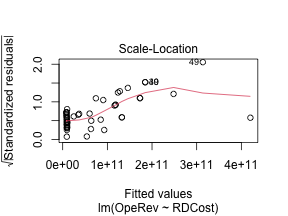<!-- --><!-- --> ??? Residuals versus fitted: 检查线性性（零均值）, Normal Q-Q: 检测正态性. Scale-Location: 检测异方差性（如果残差随着变大，则有可能异方差.) Residuals versus leverage: high residual high leverage的变量影响比较大，可以考虑删掉。the 'weighted' distance between x to the mean of x --- ## 残差检验 残差检验图 - Residuals versus fitted: 检查线性性（零均值） - Normal Q-Q: 检测正态性. - Scale-Location: 检测异方差性（如果残差随着变大，则有可能异方差.) - Residuals versus leverage: high residual high leverage的变量影响比较大，可以考虑删掉。 > leverage is a measure of how far away the independent variable values of an observation are from those of the other observations. .foot[ Ref: https://www.modernstatisticswithr.com/regression.html#model-diagnostics ] --- ## 残差检验 正态检验： - Kolmogorov–Smirnov (KS) test: ```r lillie.test(fit$residuals) ``` - Shapiro-Wilk test: ```r shapiro.test(fit$residual) ``` - Anderson-Darling test (ad.test) , Cramer-von Mises test (cvm.test)… 异方差检验：the Breusch-Pagan test ```r library(car) # Companion to Applied Regression ncvTest(fit) # ncv (non-constant variance) ``` 独立性检验: Durbin-Watson test ```r dwt(fit) # 检验自相关性 ``` --- ## 例子: CAPM Capital Asset Pricing Model，资本资产定价模型 .pull-left[ <img src="Figs/Sharpe.png" width="60%" height="100%" style="display: block; margin: auto;" /> ] .pull-right[ $$ \text(ER)_i = \text{R}_f + \beta_i (\text{ER}_m - \text{R}_f) $$ 其中 - `\(\text{ER}_i\)`: expected return of investment - `\(\text{R}_f\)`: risk free rate - `\(\beta_i\)`: beta of the investment - `\((\text{ER}_m - \text{R}_f)\)`: market risk premium ] --- ## 例子：CAPM 贝塔系数反映的是某一投资对象相对于大盘的表现情况。 - 其绝对值越大，显示其收益变化幅度相对于大盘的变化幅度越大；绝对值越小，显示其变化幅度相对于大盘越小。 - 全体市场本身的β系数为1，若基金投资组合净值的波动大于全体市场的波动幅度，则β系数大于1。反之，若基金投资组合净值的波动小于全体市场的波动幅度，则β系数就小于1。β系数越大之证券，通常是投机性较强的证券。 **公式法**：通过beta系数公式直接计算出beta结果 `\(\beta_i = (Cov(𝑟_𝑖, 𝑟_𝑚))/(𝜎_𝑚^2 )\)`； **回归法**：基于CAPM模型的数理表达式，通过回归分析估计出beta系数； --- ## 例子：CAPM ```r byd <- read_csv("../Data/002594历史数据 (1).csv") sz <- read_csv("../Data/沪深300期货历史数据 (1).csv") mt <- read_csv("../Data/600519历史数据 (1).csv") byd.ratio = as.numeric(sub("%","",byd$涨跌幅)) sz.ratio = as.numeric(sub("%","",sz$涨跌幅)) beta_1 = cov(byd.ratio,sz.ratio)/var(sz.ratio) beta_1 ``` ``` ## [1] 1.075929 ``` ```r lm1 = lm(byd.ratio~sz.ratio) lm1$coefficients ``` ``` ## (Intercept) sz.ratio ## -0.01276793 1.07592871 ``` Data Source: https://cn.investing.com/equities/byd-a-historical-data --- ## 例子：CAPM ```r ggplot(mapping = aes(x=byd.ratio, y=sz.ratio)) + geom_point() + geom_smooth(method="lm") ``` <!-- --> --- ## 例子：CAPM ```r summary(lm1) ``` ``` ## ## Call: ## lm(formula = byd.ratio ~ sz.ratio) ## ## Residuals: ## Min 1Q Median 3Q Max ## -4.4398 -0.9080 -0.1565 0.7496 6.2587 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -0.01277 0.10536 -0.121 0.904 ## sz.ratio 1.07593 0.10794 9.968 <2e-16 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 1.639 on 240 degrees of freedom ## Multiple R-squared: 0.2928, Adjusted R-squared: 0.2898 ## F-statistic: 99.35 on 1 and 240 DF, p-value: < 2.2e-16 ``` --- ## 例子：CAPM ```r plot(lm1) ``` <!-- --><!-- --><!-- --><!-- --> --- ## 例子：CAPM ```r mt.ratio = as.numeric(sub("%","",mt$涨跌幅)) lm2 = lm(mt.ratio~sz.ratio) summary(lm2) ``` ``` ## ## Call: ## lm(formula = mt.ratio ~ sz.ratio) ## ## Residuals: ## Min 1Q Median 3Q Max ## -4.1314 -0.6020 0.1011 0.6976 3.9595 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 0.03069 0.07115 0.431 0.667 ## sz.ratio 1.23138 0.07290 16.892 <2e-16 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 1.107 on 240 degrees of freedom ## Multiple R-squared: 0.5431, Adjusted R-squared: 0.5412 ## F-statistic: 285.3 on 1 and 240 DF, p-value: < 2.2e-16 ``` --- ## 画图的重要性 ```r data <- read_csv("../Data/Anscombe.csv") head(data, n=11) ``` ``` ## # A tibble: 11 × 6 ## x y1 y2 y3 x4 y4 ## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 10 8.04 9.14 7.46 8 6.58 ## 2 8 6.95 8.14 6.77 8 5.76 ## 3 13 7.58 8.74 12.7 8 7.71 ## 4 9 8.81 8.77 7.11 8 8.84 ## 5 11 8.33 9.26 7.81 8 8.47 ## 6 14 9.96 8.1 8.84 8 7.04 ## 7 6 7.24 6.13 6.08 8 5.25 ## 8 4 4.26 3.1 5.39 19 12.5 ## 9 12 10.8 9.13 8.15 8 5.56 ## 10 7 4.82 7.26 6.42 8 7.91 ## 11 5 5.68 4.74 5.73 8 6.89 ``` --- ## 画图的重要性 ```r lm1 <- lm(y1~x, data) lm2 <- lm(y2~x, data) lm3 <- lm(y3~x, data) lm4 <- lm(y4~x4, data) ``` &nbsp; 四个模型的回归结果： | | | | ------- | -------- | |观测值| 11| |x的均值| 9| |y的均值| 7.5| |回归方程| y=3+0.5x| | `\(R^2\)` | 0.667| --- ## 画图的重要性 <!-- --><!-- --><!-- --><!-- --> --- ## 多元线性回归 `$$Y = \beta_0 + \beta_1 x_2 + ... + \beta_p x_p + \epsilon$$` <img src="Figs/multi_least.png" width="1752" /> --- ## 最小二乘法 - 数据: `\((x_{i1}, x_{i2}, ..., x_{ip}; y_i)\)`, `\(i=1,2,...,n\)`. - 最小误差平方和 $$ `\begin{align*} \min_{\beta_0, \beta_1, \ldots, \beta_p} \ \sum_{i=1}^n (y_i - \hat{y}_i)^2 = \min_{\beta_0, \beta_1, \ldots, \beta_p} \ \sum_{i=1}^n (y_i - (\beta_0 + \beta_1 x_{i1}+ \beta_2 x_{i2} +...+ \beta_p x_{ip}))^2 \end{align*}` $$ 我们同样可以通过求导联立FOC得到最优解。 如果我们写成矩阵的形式 `\(\mathbf{\hat{y} = X \hat{\beta} }\)`, 此时误差平方和可以写成 $$ \min_{\beta} (\mathbf{y-X\beta})^\top (\mathbf{y-X \beta}) .$$ 此时最小二乘估计 $$ \mathbf{\hat{\beta} = (X^\top X)^{-1} X^\top y}.$$ 其中 `\((X^\top X)^{-1} X^\top\)`被称为 `\(X\)`的 Pseudo inverse. --- ## 例子 Fama-French Model .pull-left[ $$\text{ER}_i = \text{R}_f + \beta_i (\text{ER}_m - \text{R}_f) + b_s \text{SMB} + b_v \text{HML} $$ 其中： - SMB ："Small [market capitalization] Minus Big" - HML ： "High [book-to-market ratio] Minus Low"; > they measure the historic excess returns of small caps over big caps and of value stocks over growth stocks. ] .pull-right[  Ref: http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html ] --- ## 例子 Fama-French Model ```r ff_lreg = lm(AAPL.Rf ~ Mkt.RF + SMB + HML, data = data_ffex) summary(ff_lreg) ``` ``` ## ## Call: ## lm(formula = AAPL.Rf ~ Mkt.RF + SMB + HML, data = data_ffex) ## ## Residuals: ## Min 1Q Median 3Q Max ## -3.6545 -0.4038 -0.0205 0.4128 4.2533 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -0.007174 0.063591 -0.113 0.91 ## Mkt.RF 1.230826 0.059702 20.616 < 2e-16 *** ## SMB -0.447779 0.110587 -4.049 7.10e-05 *** ## HML -0.426077 0.077755 -5.480 1.15e-07 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.9537 on 222 degrees of freedom ## Multiple R-squared: 0.7316, Adjusted R-squared: 0.728 ## F-statistic: 201.7 on 3 and 222 DF, p-value: < 2.2e-16 ``` --- ## 残差分析 ```r plot(ff_lreg) ``` <!-- --><!-- --><!-- --><!-- --> --- ```r data_ffex$Rand = rnorm(nrow(data_ffex)) # generate random variables ff_lreg2 = lm(AAPL.Rf ~ Mkt.RF + SMB + HML + Rand, data = data_ffex) summary(ff_lreg2) ``` ``` ## ## Call: ## lm(formula = AAPL.Rf ~ Mkt.RF + SMB + HML + Rand, data = data_ffex) ## ## Residuals: ## Min 1Q Median 3Q Max ## -3.6458 -0.4253 -0.0308 0.4266 4.2254 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -0.005656 0.063854 -0.089 0.929 ## Mkt.RF 1.230289 0.059838 20.560 < 2e-16 *** ## SMB -0.447561 0.110805 -4.039 7.40e-05 *** ## HML -0.423674 0.078191 -5.418 1.57e-07 *** ## Rand -0.024082 0.066640 -0.361 0.718 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.9556 on 221 degrees of freedom ## Multiple R-squared: 0.7318, Adjusted R-squared: 0.7269 ## F-statistic: 150.7 on 4 and 221 DF, p-value: < 2.2e-16 ``` --- ## Adjusted R square 由于自变量个数的增加，将影响到因变量中被估计回归方程中所解释的变差数量。当增加自变量时，会使预测误差变得比较小，从而减少残差平方和 SSE，由于回归平方和 SSR=SST-SSE，当 SSE 变小时，SSR 会变大，从而 `\(R^2\)` 也会变大。如果模型中增加一个自变量，即使这个自变量在统计上并不显著， `\(R^2\)` 也会变大，为避免这种情况，提出**调整的多重判定系数(adjusted multiple coefficient of determination). ** $$ R_a^2 = 1 - \frac{\text{SSE}/(n-p-1)}{\text{SST}/(n-1)} $$ --- ## 线性回归总结 - 最小二乘法 - `\(R^2\)` 与 adjusted `\(R^2\)` - 假设检验： > F-test: 整个模型的显著性 > t-test: 单个系数的显著性 > p-value - 残差分析 --- # 有定性变量的回归 - 如果自变量是定性变量 > 引入虚拟变量 dummy variables ```r lm(y ~ as.factor(x1) + x2) ``` - 如果因变量是0-1变量 > 新业务是否会成功 > 是否批准贷款 > 明天的股票是涨还是跌 --- ## 逻辑回归 Logistic Regression  --- ## 参数估计 $$ `\begin{align*} \left\{\begin{aligned} P(Y=1) &= \frac{1}{1+ e^{-\beta_0 + \beta_1 x_1+\ldots+ \beta_p x_p}} \\ P(Y=0) &= \frac{e^{-\beta_0 + \beta_1 x_1+\ldots+ \beta_p x_p}}{1+ e^{-\beta_0 + \beta_1 x_1+\ldots+ \beta_p x_p}} \end{aligned}\right. \end{align*}` $$ 对于逻辑回归，我们不使用最小二乘法进行估计 $$ \min \sum (Y - P(Y=1))^2 $$ 我们一般使用**极大似然估计**（Maximum Likelihood Estimation, MLE) $$ `\begin{align*} \text{Likelihood} = \max \Pi_{i=1}^n \left(\frac{1}{1+z_i}\right)^{Y_i} \left(\frac{z_i}{1+z_i}\right)^{1-Y_i} \end{align*}` $$ $$ `\begin{align*} \text{Log Likelihood} = \max \sum_{i=1}^n Y_i \log \left(\frac{1}{1+z_i}\right) + (1-Y_i) \log \left(\frac{z_i}{1+z_i}\right) \end{align*}` $$ MLE的性质： 渐进无偏， 相合一致 --- ## 例子： ST预测 目标：估计上市公司是否会ST. - ST股票，意即“特别处理(Special treatment)”的股票。该政策针对的对象是出现财务状况或其他状况异常的。 - 如果哪只股票的名字前加上ST， 就是给市场一个警示，该股票存在投资风险，一个警告作用，但通常这种股票风险大收益也大. **收集的数据** | 简称 | ST | ARA | ASSET | ATO | ROA | GROWTH | LEV | SHARE | |-----|------|--------|--------|-------|-------|---------|------|----------| | 变量名 | 是否ST | 应收账款占比 | 对数资产规模 | 资产周转率 | 资产回报率 | 销售收入增长率 | 杠杆水平 | 第一股东持股比率 | --- ## 例子: ST预测 ```r data <- read_csv("../Data/ST预测.csv") str(data) ``` ``` ## spc_tbl_ [684 × 8] (S3: spec_tbl_df/tbl_df/tbl/data.frame) ## $ ARA : num [1:684] 0.1923 0.2201 0.3253 0.0257 0.5336 ... ## $ ASSET : num [1:684] 19.9 20.9 19.4 21.4 21.6 ... ## $ ATO : num [1:684] 0.0052 0.0056 0.0166 0.0028 0.2552 ... ## $ ROA : num [1:684] 0.08771 0.01682 0.04247 0.01815 0.00415 ... ## $ GROWTH: num [1:684] -0.951 -0.943 -0.937 -0.853 -0.817 ... ## $ LEV : num [1:684] 0.446 0.399 0.303 0.758 0.727 ... ## $ SHARE : num [1:684] 26.9 39.6 26.5 60.2 54.2 ... ## $ ST : num [1:684] 0 0 0 0 1 0 0 0 1 0 ... ## - attr(*, "spec")= ## .. cols( ## .. ARA = col_double(), ## .. ASSET = col_double(), ## .. ATO = col_double(), ## .. ROA = col_double(), ## .. GROWTH = col_double(), ## .. LEV = col_double(), ## .. SHARE = col_double(), ## .. ST = col_double() ## .. ) ## - attr(*, "problems")=<externalptr> ``` --- ## 例子: ST预测 <!-- --><!-- --><!-- --><!-- --><!-- --><!-- --> --- ## 例子: ST预测 <!-- --><!-- --><!-- --><!-- --><!-- --><!-- --> --- ## 例子: ST预测 ```r model.full=glm(ST~ARA+ASSET+ATO+GROWTH+LEV+ROA+SHARE,family=binomial(link=logit),data=data) summary(model.full) ``` ``` ## ## Call: ## glm(formula = ST ~ ARA + ASSET + ATO + GROWTH + LEV + ROA + SHARE, ## family = binomial(link = logit), data = data) ## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -1.4165 -0.3354 -0.2536 -0.1958 3.0778 ## ## Coefficients: ## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -8.86924 4.63586 -1.913 0.05573 . ## ARA 4.87974 1.49245 3.270 0.00108 ** ## ASSET 0.24660 0.22409 1.100 0.27115 ## ATO -0.50738 0.65744 -0.772 0.44026 ## GROWTH -0.83335 0.56706 -1.470 0.14167 ## LEV 2.35415 1.20138 1.960 0.05005 . ## ROA -0.63661 6.22354 -0.102 0.91853 ## SHARE -0.01111 0.01115 -0.997 0.31891 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## (Dispersion parameter for binomial family taken to be 1) ## ## Null deviance: 282.07 on 683 degrees of freedom ## Residual deviance: 251.51 on 676 degrees of freedom ## AIC: 267.51 ## ## Number of Fisher Scoring iterations: 6 ``` --- ## 例子: ST预测 模型选择： - 向前选择 - 向后剔除 - 逐步回归 选择的标准: - AIC准则: Akaike information criterion > `\(2k -\ln L\)`, 越小越好 - BIC准则: Bayesian information criterion > `\(k \ln n -\ln L\)`, 越小越好 --- ## 例子: ST预测 ```r model.aic=step(model.full, direction='both', trace = F) summary(model.aic) ``` ``` ## ## Call: ## glm(formula = ST ~ ARA + GROWTH + LEV, family = binomial(link = logit), ## data = data) ## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -1.4020 -0.3323 -0.2647 -0.2119 3.1063 ## ## Coefficients: ## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -4.6022 0.5646 -8.152 3.58e-16 *** ## ARA 5.1301 1.4341 3.577 0.000347 *** ## GROWTH -0.9061 0.5471 -1.656 0.097708 . ## LEV 2.5501 1.0778 2.366 0.017986 * ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## (Dispersion parameter for binomial family taken to be 1) ## ## Null deviance: 282.07 on 683 degrees of freedom ## Residual deviance: 254.04 on 680 degrees of freedom ## AIC: 262.04 ## ## Number of Fisher Scoring iterations: 6 ``` --- ## 例子: ST预测 ### ROC 曲线 接收者操作特征曲线，或者叫ROC曲线（Receiver Operating Characteristic curve） - TPR：在所有实际为阳性的样本中，被正确地判断为阳性之比率。 - FPR：在所有实际为阴性的样本中，被错误地判断为阳性之比率。 将同一模型每个阈值的 (FPR, TPR) 坐标都画在ROC空间里，就成为特定模型的ROC曲线。 --- ### ROC 曲线 ```r #install.packages("pROC") library(pROC) predicted.full <- predict(model.full, data, type="response") roc.full <- roc(data$ST, predicted.full) ggroc(roc.full) ``` <!-- --> --- ### 比较两个模型 （FULL, AIC) ```r predicted.aic <- predict(model.aic, data, type="response") roc.aic <- roc(data$ST, predicted.aic) ggroc(list(AIC=roc.aic, FULL=roc.full)) ``` <!-- -->