class: center, middle, inverse, title-slide .title[ # 财务管理理论与实务 ] .subtitle[ ## Financial Data Mining ] .author[ ### 唐润宇 ] .date[ ### 2023-10-10 ] --- # 数据挖掘 Data mining 数据挖掘(Data Mining)就是从大量的数据中，提取隐藏在其中的，事先不知道的、但潜在有用的信息的过程。 常见任务 <https://en.wikipedia.org/wiki/Data_mining> - 异常检测: 识别不寻常的数据记录，错误数据需要进一步调查。 - 关联规则学习: 搜索变量之间的关系。 - 聚类: 是在未知数据的结构下，发现数据的类别与结构。 - 分类: 是对新的数据推广已知的结构的任务。 - 回归: 试图找到能够以最小误差对该数据建模的函数。 - 汇总: 提供了一个更紧凑的数据集表示。 Ref: Data mining in R: <https://www.rdatamining.com/> --- ## 数据降维 > Human minds are good at recognizing patterns in two dimensions and to some extent in three, but are essentially useless in higher dimensions. 常见方法: - PCA 主成分分析 - ICA 独立分量分析 - kPCA 核主成分分析 - MDS 多维标度分析 &nbsp; Ref: Hastie, T., Tibshirani, R., Friedman, J. H., & Friedman, J. H. (2009). _The elements of statistical learning: data mining, inference, and prediction_ (Vol. 2, pp. 1-758). New York: springer. --- ## PCA 主成分分析是一种通过降维技术把多个变量化为少数几个主成分（综合变量）的统计分析方法。 这些主成分能够反映原始变量的绝大部分信息，它们通常表示为原始变量的某种**线性组合，且彼此不相关**。 1901年由 Karl Pearson发明。 常用的科学手段：2020年Nature中有124篇文章使用了该方法。<https://mathvoices.ams.org/featurecolumn/2021/08/01/principal-component-analysis/> --- ## PCA - 每一个主成分都是各原始变量的线性组合 - 主成分的数目大大少于原始变量的数目 - 主成分保留了原始变量的绝大数**信息** - 各个主成分之间互不相关。 -- 什么是信息？Or 什么样的变量信息量更大？ .pull-left[  ] .pull-right[  ] --- ## PCA .pull-left[ &nbsp; &nbsp; - 从不同视角观测弹簧拉长变化 - 选择最优的视角？ ] .pull-right[  ] --- ## PCA的数学定义 假设数据有p维特征 `\(\mathbf{x}=[𝑥_1,𝑥_2,…,𝑥_𝑝]′\)`, 假设我们知道其协方差矩阵为 `\(\Sigma\)`. 考虑线性组合 `$$𝑦_1=𝒂_𝟏^′ 𝒙=𝑎_{11} 𝑥_1+𝑎_{21} 𝑥_2+…+𝑎_{𝑝1} 𝑥_𝑝$$` `$$y _2=𝒂_𝟐^′ 𝒙=𝑎_{12} 𝑥_1+𝑎_{22} 𝑥_2+…+𝑎_{𝑝2} 𝑥_𝑝$$` `$$…$$` `$$𝑦_𝑝=𝒂_𝒑^′ 𝒙=𝑎_{1𝑝} 𝑥_1+𝑎_{2𝑝} 𝑥_2+…+𝑎_{𝑝𝑝} 𝑥_𝑝$$` 我们有 `\(Var(𝑦_𝒊 )=𝒂_𝒊^′ 𝚺𝒂_𝒊, Cov(𝑦_𝑖,𝑦_𝑗 )=𝒂_𝒊^′ 𝚺𝒂_𝒋\)`。 **主成分**：使得 `\(Var(𝑦_𝑖 )\)` 尽可能大的线性无关的 `\(𝑦_𝑖\)` 其中 `\((𝒂_𝒊^′ 𝒂_𝒊=𝟏)\)` 。 -- 假设p维随机向量 `\(\mathbf{x}\)` 的协方差矩阵 `\(\mathbf{\Sigma}\)` 的特征值和特征向量为 `\((\lambda_1, 𝒆_𝟏 ),(\lambda_2, 𝒆_𝟐 ),…,(\lambda_𝑝, 𝒆_𝒑 )\)`, 其中 `\(𝜆_1≥𝜆_2≥…≥𝜆_𝑝≥0\)`, 则第 `\(i\)`个主成分为 `$$𝒚_𝒊=𝒆_𝒊^′ 𝒙=𝑒_{𝑖1} 𝑥_1+𝑒_{𝑖2} 𝑥_2+…+𝑒_{𝑖𝑝} 𝑥_𝑝, \quad 𝑖=1,2,…,𝑝$$` --- ## 一些基础知识回顾 - 协方差矩阵: 是一个方阵，其 `\(i,j\)` 位置的元素是第 `\(i\)` 个与第 `\(j\)` 个随机变量之间的协方差。 $$ \Sigma_{ij} = cov(x_i, x_j) = E[(x_i - \mu_i)(x_j - \mu_j)] $$ - 有的时候我们会给数据标准化，此时对应着相关系数矩阵 `\(R\)`。 $$ R_{ij} = corr(x_i, x_j) = \frac{cov(x_i, x_j)}{\sigma_i \sigma_j}. $$ - (对称)矩阵的特征值分解(Eigendecomposition) $$ A = Q \Lambda Q^\top $$  --- ## PCA 例子 CSMAR数据库 -> 财务指标分析 -> 偿债能力 时间跨度: 2022/01/01-2023/06/30 ```r library(tidyverse) library(readxl) setwd("~/XJTU/课程/财务管理理论与实务/Codes") data = read_xlsx("../Data/FI_T1.xlsx", skip = 1) str(data) ``` ``` ## tibble [50,254 × 35] (S3: tbl_df/tbl/data.frame) ## $ 股票代码 : chr [1:50254] "没有单位" "000001" "000001" "000001" ... ## $ 股票简称 : chr [1:50254] "没有单位" "平安银行" "平安银行" "平安银行" ... ## $ 统计截止日期 : chr [1:50254] "没有单位" "2022-03-31" "2022-03-31" "2022-06-30" ... ## $ 报表类型编码 : chr [1:50254] "没有单位" "A" "B" "A" ... ## $ 行业代码 : chr [1:50254] "没有单位" "J66" "J66" "J66" ... ## $ 行业名称 : chr [1:50254] NA "货币金融服务" "货币金融服务" "货币金融服务" ... ## $ 公告来源 : chr [1:50254] "没有单位" "0.0" "0.0" "0.0" ... ## $ 流动比率 : chr [1:50254] "没有单位" NA NA NA ... ## $ 速动比率 : chr [1:50254] "没有单位" NA NA NA ... ## $ 保守速动比率 : chr [1:50254] "没有单位" NA NA NA ... ## $ 现金比率 : chr [1:50254] "没有单位" NA NA NA ... ## $ 营运资金与借款比 : chr [1:50254] "没有单位" NA NA NA ... ## $ 营运资金 : chr [1:50254] "元" NA NA NA ... ## $ 利息保障倍数A : chr [1:50254] "没有单位" NA NA NA ... ## $ 利息保障倍数B : chr [1:50254] "没有单位" NA NA NA ... ## $ 经营活动产生的现金流量净额／流动负债: chr [1:50254] "没有单位" NA NA NA ... ## $ 现金流利息保障倍数 : chr [1:50254] "没有单位" NA NA NA ... ## $ 现金流到期债务保障倍数 : chr [1:50254] "没有单位" NA NA NA ... ## $ 资产负债率 : chr [1:50254] "没有单位" "0.920637" "0.921012" "0.919335" ... ## $ 长期借款与总资产比 : chr [1:50254] "没有单位" "0.0" "0.0" "0.0" ... ## $ 有形资产负债率 : chr [1:50254] "没有单位" "0.92302" "0.923397" "0.921696" ... ## $ 有形资产带息债务比 : chr [1:50254] "没有单位" "0.0" "0.0" "0.0" ... ## $ 权益乘数 : chr [1:50254] "没有单位" "12.600355" "12.660201" "12.396993" ... ## $ 产权比率 : chr [1:50254] "没有单位" "11.600355" "11.660201" "11.396993" ... ## $ 权益对负债比率 : chr [1:50254] "没有单位" "0.086204" "0.085762" "0.087742" ... ## $ 长期资本负债率 : chr [1:50254] "没有单位" "0.0" "0.0" "0.0" ... ## $ 长期负债权益比率 : chr [1:50254] "没有单位" "0.0" "0.0" "0.0" ... ## $ 长期债务与营运资金比率 : chr [1:50254] "没有单位" NA NA NA ... ## $ 息税折旧摊销前利润／负债合计 : chr [1:50254] "没有单位" NA NA NA ... ## $ 经营活动产生的现金流量净额／负债合计: chr [1:50254] "没有单位" "0.031854" "0.03166" "0.032633" ... ## $ 经营活动产生的现金流量净额／带息债务: chr [1:50254] "没有单位" NA NA NA ... ## $ 负债与权益市价比率 : chr [1:50254] "没有单位" "0.940429" "0.940577" "0.941712" ... ## $ 有形净值债务率 : chr [1:50254] "没有单位" "11.763819" "11.825342" "11.551613" ... ## $ 固定支出偿付倍数 : chr [1:50254] "没有单位" NA NA "18.13942" ... ## $ 权益乘数2 : num [1:50254] NA 12.5 12.6 12.4 12.5 ... ``` --- ## PCA 例子 整理数据: - 选取每个公司最新的数据 - 转换数据格式 - 删掉非数字的变量 - 删掉NA的公司 ```r PCA_data <- data |> group_by(股票代码) |> slice(which.max(as.Date(统计截止日期, '%Y-%m-%d'))) |> ungroup() |> type_convert() |> select(-c(1:7)) |> drop_na() # str(PCA_data) ``` --- ## PCA 例子 在做PCA之前，我们可以观察一下我们的数据的相关系数矩阵 ```r names(PCA_data) <- c(1:length(PCA_data)) cor.mat <- cor(PCA_data) library("corrplot") corrplot(cor.mat, type="upper", order="hclust", tl.col="black") ``` <img src="lecture2_files/figure-html/unnamed-chunk-3-1.png" style="display: block; margin: auto;" /> --- ## PCA 例子 我们使用**FactoMineR**帮助我们做PCA ```r library(FactoMineR) pca.res <- PCA(PCA_data) ``` <!-- -->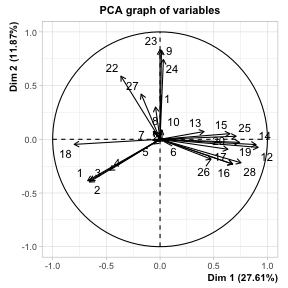<!-- --> --- ## PCA 例子 ```r library(factoextra) fviz_screeplot(pca.res) ``` 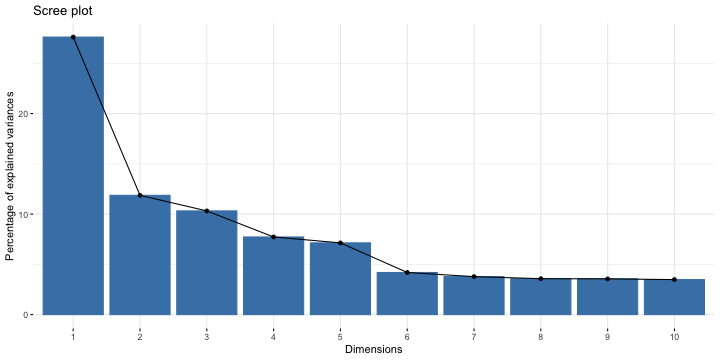<!-- --> --- ## PCA 例子 PCA的结果里面有很多东西，比如我们通常比较关注的特征值和特征向量。 ```r pca.res <- PCA(PCA_data, ncp=5, graph=FALSE) round(pca.res$eig, 3) ``` ``` ## eigenvalue percentage of variance cumulative percentage of variance ## comp 1 7.732 27.614 27.614 ## comp 2 3.324 11.870 39.484 ## comp 3 2.889 10.319 49.803 ## comp 4 2.163 7.726 57.529 ## comp 5 1.999 7.139 64.669 ## comp 6 1.174 4.193 68.862 ## comp 7 1.059 3.782 72.643 ## comp 8 1.001 3.576 76.220 ## comp 9 0.996 3.559 79.779 ## comp 10 0.976 3.487 83.265 ## comp 11 0.866 3.094 86.359 ## comp 12 0.834 2.978 89.337 ## comp 13 0.520 1.856 91.193 ## comp 14 0.434 1.548 92.742 ## comp 15 0.385 1.375 94.117 ## comp 16 0.329 1.174 95.291 ## comp 17 0.302 1.080 96.371 ## comp 18 0.270 0.965 97.335 ## comp 19 0.223 0.796 98.131 ## comp 20 0.148 0.530 98.661 ## comp 21 0.126 0.450 99.112 ## comp 22 0.075 0.270 99.381 ## comp 23 0.062 0.222 99.603 ## comp 24 0.058 0.209 99.812 ## comp 25 0.031 0.112 99.923 ## comp 26 0.019 0.068 99.991 ## comp 27 0.003 0.009 100.000 ## comp 28 0.000 0.000 100.000 ``` --- ## PCA的应用 --- 图片压缩 .pull-left[ 一张图片是由三原色(RGB)叠加出来的。 每个颜色下面都是一个矩阵，矩阵的维度就是我们常说的像素数。 例: 某遥遥领先品牌新机： <https://consumer.huawei.com/cn/phones/mate60-pro/specs/> - 后置摄像头： 5000 万像素超光变摄像头 - 后置摄像头照片分辨率: 最大可支持 8192 × 6144 像素 ] .pull-right[ <img src="Figs/RGB.png" width="1371" /> ] --- ## PCA的应用 --- 图片压缩 .pull-left[ <img src="Figs/xjtu_lib.png" width="951" /> ] .pull-right[ 我们尝试着压缩一张钱学森图书馆的图片。 ```r library(png) image <-readPNG("../Data/xjtu.png") str(image) ``` ``` ## num [1:535, 1:713, 1:3] 0.886 0.886 0.886 0.886 0.886 ... ``` 原图的大小为535*713. ] --- ## PCA的应用 --- 图片压缩 .pull-left[ <img src="xjtu_10.png" width="951" /> 主成分数量 = 10 ] .pull-right[ <img src="xjtu_50.png" width="951" /> 主成分数量 = 50 ] --- ## PCA的应用 .pull-left[ - 78000岁的尸骨墓穴 - 如何确定是“墓穴”呢？ - 骨头周围的泥土成分和周围成分泥土成分显著不同！ - 80 个土壤样本 - 每个样本中13维信息（Si, K, Ca, Ti, Mn, Fe, Zn, Ga, As, Rb, Y, Zr and Ba） .foot[Earliest known human burial in Africa，published in _Nature_ on May 5, 2021] ] .pull-right[ <img src="Figs/PCA_burial.png" width="1133" /> ] --- ## PCA的应用 <img src="Figs/FirmPCA.png" width="1605" height="280px" /> > 白重恩等. 中国上市公司治理结构的实证研究[J]. 经济研究 , 2005, 11. > 张学勇,廖理.股权分置改革、自愿性信息披露与公司治理[J].经济研究, 2010, 45(04): 28-39+53. > 胡楠,薛付婧,王昊楠.管理者短视主义影响企业长期投资吗？——基于文本分析和机器学习[J].管理世界, 2021, 37(05):139-156+11+19-21 --- ## PCA 的局限性 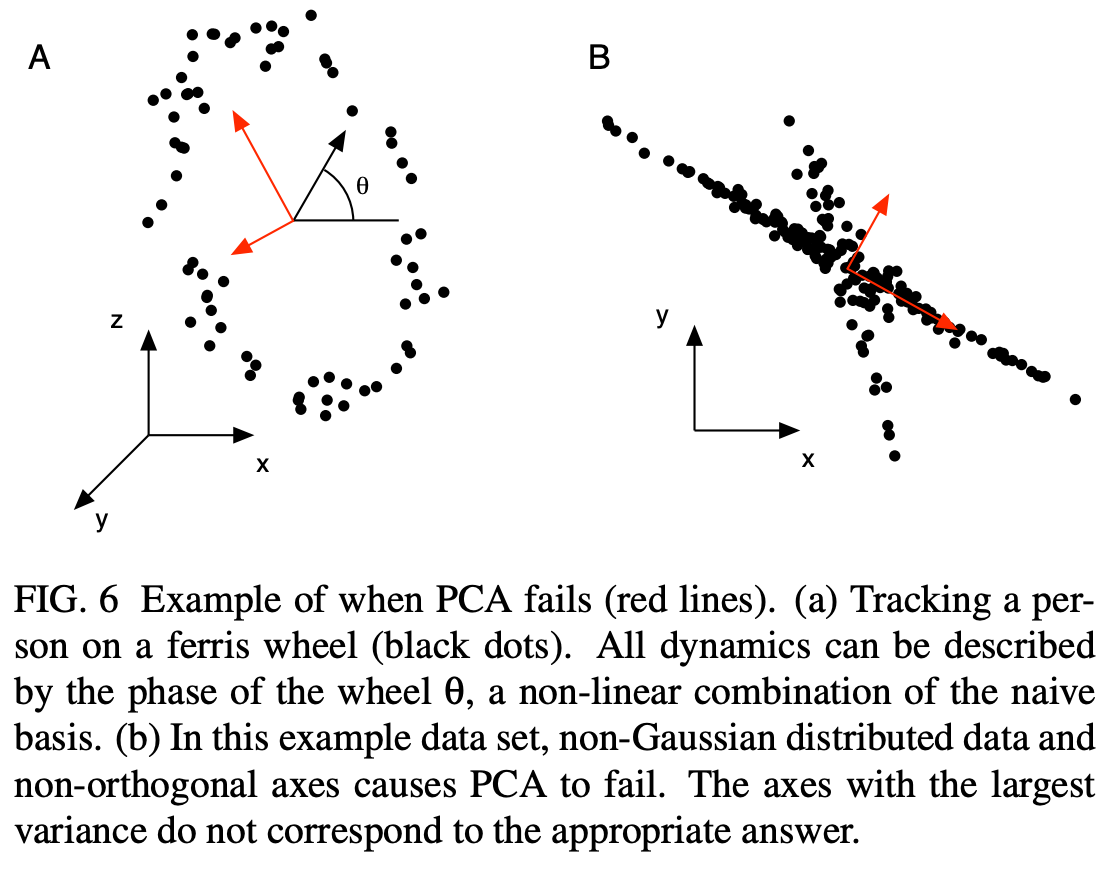 --- ## 其他数据降维方法 - kPCA: 将线型函数使用核函数(kernal)变成非线性，可以描述更加复杂的关系 kernlab::kpca - ICA: 放松PCA中的不同主成分需要线性无关的假设 ica::ica - MDS: Multidimensional scaling 我们有n个观测值 `\(x_1, \ldots, x_n \in \mathbb{R}^p\)`, 每个观测值是 p 维的，那么MDS需要找到一组投影 `\(z_1, \ldots, z_n \in \mathbb{R}^k\)`, `\(k<p\)` 使得下面的stress function取得最小。 `$$\min_{z_1, \ldots, z_n} \ \sum_{i \neq j} (d_{ij} - \Vert z_i-z_j \Vert)^2.$$` 实际上就是找一个低维的投影，但是能够维持原数据之间的间隔。 如果我们取 `\(d_{ij} = \langle x_i -\mu_i, x_j - \mu_j \rangle\)`, 那么此时MDS就与PCA一样了。 我们可以使用R语言中的**cmdscale**函数实现MDS. --- ## 聚类分析 - 分类: 有监督学习 - 聚类: 无监督学习 All relate to grouping or segmenting a collection of objects into subsets or "clusters", such that those within each cluster are more closely related to one another than objects assigned to different clusters. 常见的聚类方法： > K-means: 基于距离的聚类 > DBSCAN: 基于密度的聚类 > Hierachical Clustering: 层次化聚类方法 --- ## K means 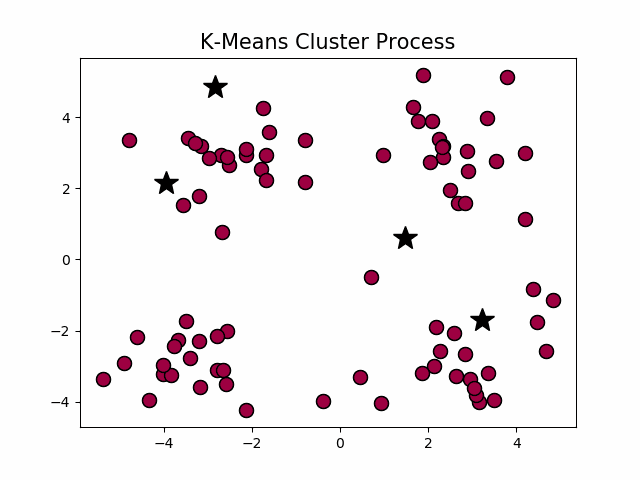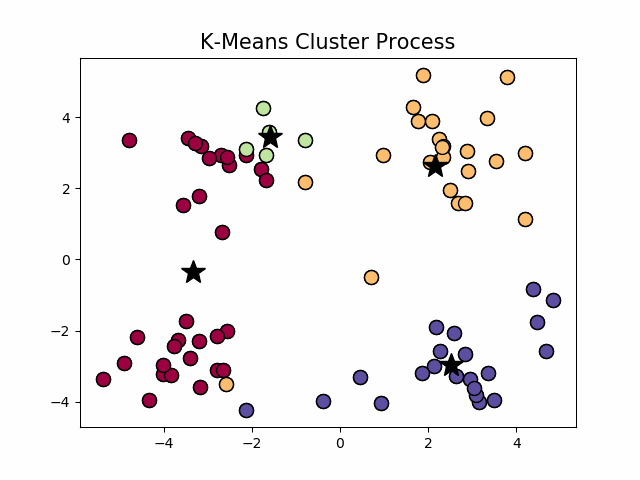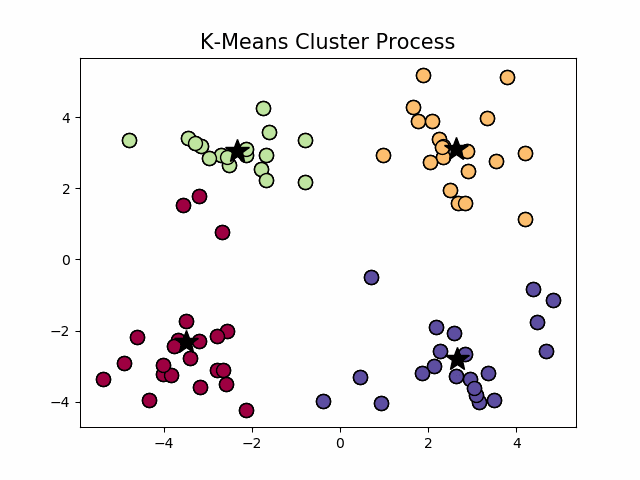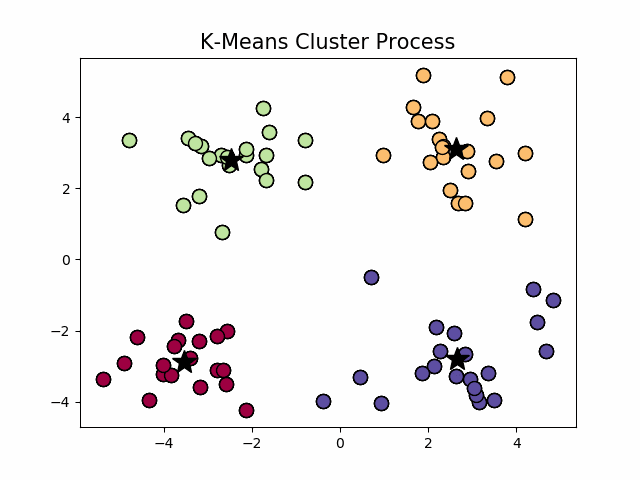 --- ## DBSCAN  ??? 需要两个参数, `\(\epsilon\)` 半径大小 和 minpts 每个簇里面点个数 - Find core samples of high density - Expand clusters from core samples - Assign noise samples to nearest cluster 不用给类别数量 --- ## Agglomerative 层次聚类 .pull-left[  ] .pull-right[  ] ??? Dendrogram: a tree-like diagram used to illustrate the arrangement of the clusters produced by hierarchical clustering. - Agglomerative: bottom-up approach, each observation starts in its own cluster, and clusters are successively merged together. - Divisive: top-down approach --- ## 常见聚类算法比较 上述常见的聚类算法有着不同的优缺点，我们需要针对数据的不同选择合适的方法。 当然我们也可以都试试看~ &nbsp; | 算法 | 数据类型 | 抗噪点 | 聚类形状|算法效率 | | ------- | -------- | -------- | --------| -------- | | K-means | 混合型 | 较差 | 球形 | 很高| | DBSCAN | 数值型 | 较好 | 任意形状 | 一般| | Agglomerative | 混合型 | 较好 | 任意形状 | 较差| --- ## 例子 K-means 效果 ```r library(cluster) fviz_nbclust(PCA_data, kmeans, method = "wss", k.max=20) km <- kmeans(PCA_data, centers=14) fviz_cluster(km, data = PCA_data) ```  --- ## 例子 DBSCAN 效果 ```r library(fpc) db <- dbscan(PCA_data, eps =200000000) fviz_cluster(db, data = PCA_data) ``` <!-- --> --- ## 例子 Agglomeration 效果 ```r distance <- get_dist(PCA_data, stand=TRUE) hcl <- hclust(distance, method = "complete") plot(hcl, labels=FALSE) hc_cut <- hcut(distance, k=10, hc_method = "complete") fviz_cluster(hc_cut, data = PCA_data) ``` 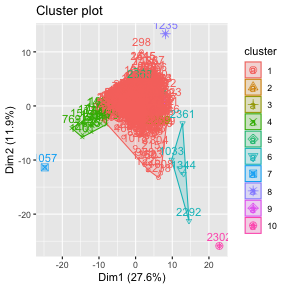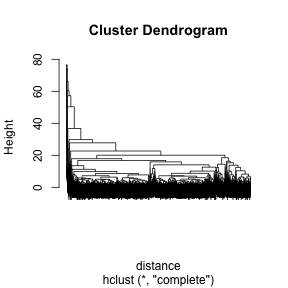 --- # 文本挖掘 我们的财务数据里面也有很多例如公司简介的文本信息，我们可以使用R对这些文本进行分析。  ```r data <- read_csv("../Data/IRR_ListedInfo.csv") newdata <- data |> select(ShortName, CompanyProfile) |> drop_na() ``` Ref: <https://www.tidytextmining.com/> --- ```r test <- newdata$CompanyProfile library(jiebaR) library(tm) library(tmcn) library(wordcloud2) cutter = worker() # we can add more options here test_seg = segment(test, cutter) test_df = data.frame(table(test_seg)) new_df <- test_df |> filter(Freq > 1) wordcloud2(new_df) ``` <div class="wordcloud2 html-widget html-fill-item-overflow-hidden html-fill-item" id="htmlwidget-de2fc16e16c2883c26dd" style="width:576px;height:216px;"></div> <script type="application/json" data-for="htmlwidget-de2fc16e16c2883c26dd">{"x":{"word":["03","1","1.5","10","100","1000","11","110","12","120","13","14","146","15","150","16","1600","17","18","180","19","1994","1995","1996","1997","1998","1999","2","20","200","2000","2001","2002","2003","2004","2005","2006","2007","2008","2009","2010","2011","2012","2013","2014","2015","2016","2017","2018","2019","2020","2021","2022","21","22","220","23","24","25","25000","26","27","28","29","3","3.0","3.2","30","300","30000","31","32","4","40","400","44","5","50","500","5000","50000","6","60","600","6000","60000","65","7","7.0","70","700","71","8","80","800","8000","9","90","9001","93","99","A","A1","AAA","ab","ABB","AI","AL2O3","ANSI","AoA","AS","ASME","AUDIOWELL","BDO","Bianco","BRC","C","CCG","CE","CMA","CMMI","CMMI5","CNAS","CPU","CPUIP","CQC","CRM","CRO","CSA","D","DCS","DNV","EGG","ERP","ETL","Evertie","F","FDA","FPC","FPGA","FSSC22000","G","G20","GB","GC1","GE","GMP","Google","GROUP","HACCP","HIPS","HK","I","IATF16949","IBM","IC","IP","IS09001","ISO","ISO13485","ISO14001","ISO22000","ISO45001","ISO9001","IT","K","kV","L","LCD","LCM","Led","LED","LG","LNG","LTD","M","㎡","MAX","MES","Mini","Monte","nm","NZS","OA","ODM","OEM","OHSAS18001","OLED","OPENMASK","P","PCB","PCBA","PLM","PQS","QS","REACH","RedPrime","RISC","ROHS","S","SANOVO","SFDA","SH","SMA","SMT","SoC","SZ","T","T28001","TC38","TCL","THUNDEROBOT","TS16949","UL","V","一","一个","一体","一体化","一大批","一如既往","一定","一家","一带","一批","一支","一期","一条龙","一次","一次性","一汽","一流","一直","一种","一站式","一等奖","一类","一系列","一级","一致","一致性","一贯","一路","七丰","万","万件","万余","万元","万台","万吨","万套","万平方米","万控","万朗","三","三元","三十","三大","三大类","三家","三星","三板","三标","三祥","三等奖","三级","三维","三项","上","上半年","上市","上市公司","上海","上海交通大学","上海市","上游","上述","下","下属","下游","下设","下辖","不","不同","不懈","不断","不断丰富","不断创新","不断加强","不断完善","不断扩大","不断更新","与","专业","专业化","专利","专利技术","专利权","专家","专有","专注","专用","专用设备","专科","专精","专门","专项","专项资金","且","世博会","世界","世界各地","世界级","世纪","业","业内","业务","业务范围","业界","业绩","东","东北","东南亚","东微","东方","东莞","丝绸","两","两个","两化","两大","两大类","两岸","严格","严格执行","严格把关","丽","个","个人","个性化","个省","中","中医","中华人民共和国","中国","中国人民银行","中国电信","中国科学院","中国移动","中国联通","中小","中小企业","中心","中汽","中海","中石化","中粮","中纺","中药","中试","中车","中间体","中青年","丰安","丰富","临床","临床试验","丹麦","为","为主","为了","为本","为辅","为魂","主","主体","主动","主导","主导产品","主机厂","主板","主流","主营","主营业务","主要","乃至","之","之一","之本","之路","之间","乌鲁木齐","乐清市","乘用车","也","了","事业","事业部","二","二十余年","二十多年","二十年","二氧化硅","二等奖","于","云","云计算","云里","互动","互联","互联网","五","五大","五年","五环","五级","五金","亚","亚信","亚洲","亚虹","亚通","交互","交付","交叉","交流","交通","交通运输","产","产业","产业化","产业园","产业基地","产业链","产品","产品出口","产品品质","产品开发","产品种类","产品类别","产品线","产品组合","产品设计","产品质量","产品销售","产学研","产物","产能","亩","享有","京东方","京广","人","人力","人员","人工智能","人性化","人才","人才培养","人才队伍","人数","人民","人民币","人民政府","人民银行","人类","人群","亿","亿元","亿能","仅","今后","从","从业","从事","从而","仓储","他","他们","代理","代码","代维","代表","代表性","代谢","以","以上","以上学历","以下","以人为本","以及","以来","以银复","仪","仪器","仪器仪表","仪器设备","仪表","件","价值","价值观","任务","仿制","仿真","企业","企业名单","企业级","众","众多","众诚","优于","优势","优化","优异","优秀","优秀企业","优胜","优良","优质","优质产品","优越","伙伴","会","会员单位","会议","传动","传媒","传感","传感器","传播","传统","传输","位","位于","位列","位居","低","低功耗","低压","低温","体","体现","体系","体育","体验","体验式","何伟","何氏","余","余个","余亩","余人","余台","余家","余平方米","余年","余种","余项","佛山","佛山市","作为","作出","作用","佳合","使","使命","使得","使用","供应","供应商","供应链","供货","依托","依据","依法","依靠","便利","便捷","便携式","促进","促销","俄罗斯","保","保健","保健品","保健食品","保密","保持","保证","保证体系","保险","保障","保驾护航","信","信任","信创","信号","信息","信息产业","信息化","信息安全","信息技术","信息系统","信息网络","信用","信誉","信赖","信达","信道","修订","借力","借助","倡导","偏光片","做","做出","健全","健康","健身","储备","储能","催化剂","元","元件","元器件","元素","元道","充分","充分利用","充分发挥","充电","兆","先发","先后","先导","先行","先进","先进设备","光","光伏","光学","光电","光纤","光谱","光通信","光频","克拉","免疫","党组织","入围","入库","入选","全","全世界","全体","全员","全国","全国性","全套","全方位","全球","全球化","全球排名","全自动","全资","全过程","全部","全面","全面推行","八","公共","公共安全","公司","公司总部","公布","公开","公益","六十多个","六大","六项","兰州","兰州市","共","共创","共同","共建","共生","共计","共赢","关注","关系","关键","关键因素","关键技术","关键设备","其","其中","其他","其它","具","具体","具备","具有","典型","养殖","兼容","兼顾","内","内外","内容","内核","内生","内部","内部管理","内销","再生","最","最优","最佳","最具","最大","最新","最终","最高","军信","军工","农业","农产品","农作物","农牧","冠军","冠龙","冬奥","冬奥会","冰箱","冰箱门","冲压","冲压件","决策","冶金","冷","冷冻干燥","冷凝器","冷却","冷却塔","冷器","冷风","净化","净化系统","准","准备","准确","凌","减少","减排","几年","凭借","凭借着","凯华","出","出口","出货量","出资","分为","分会","分公司","分别","分子","分子生物学","分子筛","分支机构","分散","分析","分析仪器","分选","列入","则","创","创业","创业板","创始","创建","创意","创意设计","创新","创新型","创新奖","创新性","创新能力","创立","创耀","创造","初","初期","判读","利用","利益","到","制","制作","制冷","制剂","制动","制品","制备","制定","制度","制成","制氧机","制种","制程","制药","制订","制造","制造业","制造厂","制造商","刺激","剂","前","前列","前沿","前沿技术","前瞻性","前装","前身","副会长","副理事长","副董事长","力","力争","力佳","力度","力量","办事处","办公","功率","功能","功能性","加","加大","加工","加工能力","加强","加快","加热","务实","动力","动力电池","动态","助力","助学","努力","劳动","势","势力","勘查","包括","包装","包装机","包装袋","化","化及","化合物","化妆品","化学","化学品","化工","北京","北京市","北汽","北美","匠心","区","区位","区域","医用","医疗","医疗器械","医疗机构","医药","医药企业","医院","十三","十余年","十几年","十分","十四五","十堰","十多年","十大","十强","升级","半","半导体","半导体器件","华","华为","华南","华岭","华康","华星","华电","华硕","华能","华融","协","协会","协会会长","协作","协同","协议","卓越","单一","单位","单元","单项","南","南京","南京市","南水北调","南沙","南美","博士","博士后","博览会","占","占地","占地面积","占据","卡","卫星","卫生","印刷","印度","即","即将","却","厂","厂区","厂商","厂家","厂房","厅","历史","历年","历经","压力","压力容器","压缩机","原","原则","原创","原厂","原料","原料药","原材料","厦门","厨房","参与","参数","参股","又","叉车","及","及其","及时","双","双赢","反应器","反馈","发动机","发展","发展前景","发展趋势","发布","发挥","发改委","发明","发明专利","发现","发电","发行人","发行股票","发起","发达","发酵","取代","取得","取胜","受到","受理","变化","变压器","变电站","变矩器","变速箱","变革","口碑","古镇","另","只为","可","可为","可以","可信赖","可控","可能","可达","可靠","可靠性","台","台州市","号","号文","号楼","各","各个","各个环节","各地","各大","各种","各类","各项","合作","合作伙伴","合作项目","合同","合富","合成","合成树脂","合格","合格率","合理","合肥","合肥市","合规","合资","合金","吉林省","同","同时","同步","同类","同类产品","同行业","名","名列前茅","名单","名牌","名牌产品","名称","后","向","吨","吸引","吸收","吹","员工","周到","周年","和","和谐","和顺","咨询","咨询机构","品","品格","品牌","品牌价值","品牌优势","品牌形象","品种","品类","品质","哈尔滨","响应","售前","售后","售后服务","唯一","唯科","商","商业","商业化","商业银行","商务","商号","商品","商圈","商家","商标","商用车","商超","嘉兴市","嘉善县","嘉奖","嘉戎","器","器件","器具","器械","四","四位一体","四大","四川","四川省","回报","回馈","因素","团体","团结","团队","园区","围绕","固","固体","固定","固废","国","国产","国产化","国内","国内外","国务院","国外","国家","国家专利","国家标准","国家火炬计划","国家电网","国家科技部","国家级","国有","国电","国网","国航","国芯","国资委","国防","国际","国际化","国际品牌","国际机场","国际标准","国际航运","图像","土壤","在","在于","在内","在建","在技术上","在线","地","地下水","地为","地位","地区","地图","地处","地带","地方","地理","地理位置","地理信息","地理信息系统","地质灾害","地铁","场地","场强","场景","均","坐落","坐落于","坚定","坚定不移","坚实","坚持","坚持不懈","垃圾","垄断","型","型式","城市","城镇","城际","培养","培育","培训","培训基地","基","基于","基因","基地","基康","基建","基本","基石","基础","基础设施","基站","基金","基金会","塑","塑料","塑料包装","塑造","填埋","填补","境内","增值","增加","增强","增长","增长点","壹级","处于","处理","处置","备案","复合","复合材料","复杂","外","外包","外观","外观设计","外购","外销","多","多个","多元","多元化","多台","多名","多家","多平方米","多年","多所","多方面","多晶硅","多条","多样化","多次","多款","多种","多项","大","大众","大分子","大力","大力发展","大唐","大型","大学","大学生","大户","大族","大桥","大湾","大禹","大胆","大街","大规模","大连","大道","大量","大陆","天","天下","天地","天岳","天津","天津市","天润","天然","天然气","天猫","天益","天纺标","天铭","太湖","太阳能","夯实","头部","奉献","奉行","奋斗","奔","奔朗","奔驰","契机","奕","奖","奖项","套","奠定","奥迪","好","好评","如","如今","妈妈","始建","始终","始终如一","委","委会","委员","委员会","威","威海","威海市","威胁","媒体","子公司","存储","存在","孚","学习","学会","学历","学术","学科","孵化","宁波","宁波市","它","守","守信","守护","守法","安全","安全卫生","安全可靠","安全性","安徽","安徽省","安装","安防","完全","完善","完备","完成","完整","完美","宏碁","宗旨","定义","定位","定制","定向","宝","实业","实力","实施","实朴","实现","实用新型","实践","实践经验","实际","实验","实验室","宠","宠物","宠物市场","宠物用品","宠物食品","审核","客商","客户","客户服务","客户资源","客运站","室内","家","家人","家子","家庭","家用","家用电器","家电","宽禁带","宾馆","密切","密封","富士","富阳","富饶","对","对于","对外贸易","对接","寻求","导体","导光板","导入","导向","导热","导电","导航","封装","将","射频","小","小家电","小批量","小米","小试","少数","尖端","就","就是","就近","尺寸","尼龙管","局","层","居","居于","屏障","展开","展望未来","展示","属","属于","屡次","履行","山","山东","山东省","山西","山西省","岩土","峰会","崛起","嵌入式","工","工业","工业化","工业协会","工业园","工业园区","工作","工作站","工信部","工具","工厂","工序","工控","工程","工程化","工程塑料","工程师","工程技术","工程施工","工程机械","工程项目","工艺","工艺水平","工艺流程","左右","巨人","巨大","巨头","巩固","差异化","已","已有","已经","已获","巴斯夫","巴氏","巴西","市","市区","市场","市场份额","市场占有率","市场竞争","市场经济","市场需求","市政","市级","市长","布局","希望","希荻","带","带动","带头人","带来","带领","帮助","常务理事","常州","常熟","干散货","平原","平台","平方米","平板","平米","平衡","年","年产","年产值","年初","年底","年度","年来","年版","年销售额","并","并且","并于","并进","幸福生活","广","广东","广东省","广大","广大客户","广州","广州市","广泛","广泛应用","广达","广阔","床","库","应急","应用","应用领域","底","庞大","废水","废水处理","座","康","康冠","康复","康普","延伸","廷","建成","建有","建材","建立","建筑","建筑面积","建设","建设工程","建设部","建设项目","开关","开创","开发","开发区","开发新","开启","开始","开展","开拓","开拓创新","开拓进取","开放","开采","式","引入","引导","引进","引领","引领者","张江","强","强劲","强化","强国","强大","强有力","当时","形势","形式","形态","形成","彩晶","影响","影响力","得到","循环","微","微型","微波","微生物","微电子","微粉","德","德国","德州","心","志愿","快","快乐","快捷","快速","快速反应","态势","态度","思想","性","性能","总","总成","总资产","总部","恒","恒立","恩","恩威","患者","您","情况","情报","惠","惠丰","惠州","惠普","意义","意大利","意识","感应","感知","愿","愿景","慈善","懂","成","成为","成功","成员","成品","成型","成套","成就","成本","成果","成熟","成熟度","成立","成绩","成都","成都市","成长","成长性","我","我们","我司","我国","或","战略","战略性","战略目标","截止","截至","戴尔","户外","房产","所","所属","所有","所有制","手段","打","打破","打通","打造","打造出","扣式","执行器","扩大","扩孔","扩展","扩张","扬声器","批件","批准","批量","批量生产","承包","承担","承继","承诺","技改","技术","技术人员","技术创新","技术含量","技术实力","技术开发","技术开发区","技术指标","技术支持","技术改造","技术标准","技术水平","技术装备","技术规范","技术革新","技能","把","投产","投入","投资","投资者","投资银行","抗","抗击","抗毒素","抗血清","护理","报","报告","担当","拓展","招标","拜","拟态","拥有","拼搏","持有","持续","持股","挂牌","指令集","指导","指引","指数","指标","按","按摩","按照","挑战","挖掘","振兴","换热器","授予","授权","掌握","排名","排名第","排头兵","排放","探测器","探索","接入网","接轨","控","控制","控制器","控制系统","控系统","控股","推出","推动","推广","推广应用","推荐","推行","推进","掩膜","提交","提供","提供商","提出","提升","提取","提高","搜索","搭建","携手","摄像头","摩托车","撬装","播恩","操作","擎","支持","支援","支撑","收入","收益率","收获","收购","改制","改变","改善","改性","改良","改装","改进","改造","改革","改革开放","攻克","政务","政府","政府部门","政策","效应","效率","效益","教","教学","教育","敢","数","数亿元","数创","数十家","数十年","数字","数字化","数据","数据中心","数据分析","数据处理","数据库","数据管理","数控","数智","数模","数百个","整个","整体","整合","整形","整机","整理","整肠丸","整车","整车厂","文化","料","料于","新","新一代","新兴","新兴产业","新冠","新区","新品","新品种","新型","新威凌","新工艺","新材","新疆","新能源","新芝","新药","方向","方式","方案","方案设计","方法","方盛","方针","方面","施工","旗下","无人机","无线","无线电","无线通信","无菌","无锡","无锡市","既有","日","日化","日本","日用塑料","日经","旨在","早","时代","时间","昆山","昆明","明天","明星","明显","明确","星","春光","是","显示","显示器","显著","晋级","晨光","普","景","晶","智","智慧","智能","智能化","智能家居","智造","暂降","曙光","更","更为","更加","更名","更好","更是","曾","替代","月","月在","有","有关","有序","有效","有机","有机颜料","有色","有色金属","有限公司","有限责任","朋友","服务","服务业","服务体系","服务商","服务器","服务型","服务奖","服务平台","服务提供商","服务网络","服务质量","服务项目","服装","服饰","朗","期","期内","期待","期货","木渎镇","未","未来","本","本地化","本着","机","机制","机加工","机器","机器人","机场","机床","机房","机构","机柜","机械","机械工程","机械配件","机遇","杀菌","杂志","权","权威","权威认证","权属","材料","条","来","来自","极","极具","极致","极高","杭州","杭州市","杯","杰创","松下","松江","板","板块","构建","构筑","架构","柏星龙","柔性","柔性化","柘城","标","标准","标准化","标杆","标识","树立","树脂","校企","校准","样品","样本","核","核发","核心","核心成员","核心技术","核心部件","核电","根据","根本","格","格力","格局","桩","桩基","梦","检","检修","检查","检测","检疫","检验","植保","植物","概念","槽车","模具","模具设计","模块","模块化","模型","模塑","模式","模拟","模组","橡","橡塑","橡胶","次氯酸钠","欧","欧康","欧普泰","欧洲","欧盟","欧福","欧美","正","正在","正式","正极","此外","步伐","武汉","殊荣","残奥会","母公司","每","每个","每年","比","比亚迪","比例","比依","比武","毗邻","民族","民生","民营","民营企业","气","气体","氢","氢气","氢氧化钾","氢氧化铝","氢能","氧化铝","氩","氯","水产饲料","水准","水利","水利工程","水平","水电站","水疗","永恒","永续","永远","求生存","汇聚","汇集","江宁区","江苏","江苏省","江西","江西省","江门","江阴市","污","污染","污水","污水处理","污泥","汽","汽车","汽车空调","汽车行业","沈阳","沉淀","沟通","河北","河北省","河南","河南省","油","油气","油炸锅","治理","治疗","治疗仪","沿海","泌尿","法","法人","法国","法律法规","注册","注册资本","注册资金","注塑","注塑件","注塑模","注射","注射器","注射液","注重","泰","泰州","泰德","泰恩康","泰慕士","洁净","洁食","洛阳","洛阳市","洞察","活动","活性剂","活跃","流","流感疫苗","流程","测绘","测试","测试仪","测量","济南","浙江","浙江大学","浙江省","浦东新区","浦湘","浮选","海","海事局","海信","海内外","海南","海外","海宁市","海尔","海康","海正","海泰新能","海洋工程","海西","海通","涂料","消化道","消费","消费品","消费类","消费者","涉及","液体","液力","液压","液态","液晶","液晶显示","涵盖","淬火","深交所","深入","深厚","深受","深圳","深圳市","深圳证券交易所","深度","深耕","混凝土","混合","添加剂","清洁","清越","渗","渠道","温州","港口","港珠澳","湖北","湖北省","湖南","湖南省","湿法","满意","满意度","满足","滤液","滨州市","滩","滚刀","潜力","澳大利亚","激光","激励","激烈","火神","灿能","炸锅","点","烟台","烤箱","热","热交换器","热塑性","热处理","热循环","热熔","热熔胶","焊","焊丝","焊接","焊接机","焊机","焊材","焚烧","煮蛋","煤","煤化工","煤炭","照明","熔炼","熔焊","熟食","燃料","燃气","燃油","爱","爱心","片","版","版图","牌","牢固","牢牢","物","物料","物流","物理","物资","物里","特","特别","特征","特新","特殊","特点","特种","特种橡胶","特色","特许","独特","独立","独角兽","猫","率先","玉米","玖","玩具","环保","环保型","环境","环境保护","环境友好","环渤海","环节","现","现代","现代化","现名","现场","现实","现已","现有","玻璃","玻璃体","珠三角","珠海","珠海市","球蛋白","理事会","理事单位","理事长","理工","理工大学","理念","理论","瑞奇","瑞奇智造","瑞斯","瓶级","瓶装","甘肃省","生产","生产商","生产工艺","生产线","生产能力","生命","生命周期","生命科学","生存","生态","生殖系统","生活","生物","生物制品","生物制药","生物医药","生物科技","用","用于","用户","用户至上","用水","用药","用钢","由","由于","甲级","申报","申请","电","电信","电力","电力线","电力设备","电动","电动绞盘","电压","电商","电器","电子","电子产品","电子信息","电子商务","电子市场","电子电器","电子科技","电子线","电子行业","电工","电机","电极","电气","电池","电源","电磁","电视","电线","电缆","电能","电解","电镀","畅销","留人","畜牧","畜牧业","疗","疫情","疫苗","疾病","痛点","登记","登陆","白","白内障","白鹤","百","百个","百家","百年","百强","百项","的","盈利","益处","益生菌","盐酸","监控","监测","监测技术","监督","盛","目前","目录","目标","直接","直流","直辖市","相关","相应","相结合","相继","盾构","省","省份","省内","省市","省级","省部级","真空","真空包装","真诚","眼","眼科","眼科医院","眼镜","着","着力","瞄准","瞪","知名","知名企业","知名品牌","知名度","知识","知识产权","短短的","石化","石家庄","石油","石油化工","石油大学","石油机械","石英","石英玻璃","矿业","矿产","矿产资源","矿山","矿物","矿石","研","研制","研发","研究","研究成果","研究所","研究生","研究院","砖","破伤风","破岩","破碎","硅","硅橡胶","硅烷","硕士","硫辛酸","硬","硬件","确保","碱性","碳","碳化硅","碳性","磁共振","磁塑","磨料","磨边","磷脂","磷酸","示范","社会","社会各界","视觉","视频","神经","神马","福布斯","福建","福建省","离合器","离子","禽肉","私营企业","秉承","秉持","秉持着","种业","种子","种类","科","科学","科学仪器","科学城","科学技术","科技","科技厅","科技园区","科技型","科技成果","科技股份","科技进步","科技部","科润","科研","科研单位","科研成果","科研机构","科研院所","科研项目","积极","积极探索","积累","称号","称重","移动","税收","稳健","稳定","稳定性","稳居","稳步","稳步发展","空","空气","空白","空调","空间","穿戴","穿越","突出","突出贡献","突破","窑","立业","立体","立式","立志","立航","立足","立足于","立项","竞争","竞争力","竞技","竞赛","竭尽全力","端","端子","笔记本电脑","符合","第一","第一家","第一款","第三代","第三批","第三方","第二","第二届","第二批","等","等奖项","等等","策略","签订","简称","箔","算法","管","管及","管接头","管控","管理","管理体系","管理制度","管理局","管理层","管理手段","管理方面","管理模式","管理水平","管理系统","管线","管道","箱式","类","类产品","类似","类型","粉","粉体","粉末冶金","粉末涂料","粘性","粘接","粤港澳","粮食","精准","精品","精密","精工","精度","精微","精湛","精益","精益求精","精神","精神障碍","精细","精细化","精细化工","精耕细作","精选","糖","糖醇","系","系列","系列产品","系统","系统化","系统地","系统工程","系统结构","系统集成","紧固件","紧密","紧紧围绕","紧跟","累计","繁育","纤维","约","级","纬","纯化","纳入","纳税","纳米","纺织","纺织品","纽泰格","线","线上","线下","线圈","线缆","线路板","组","组件","组建","组成","组织","组网","组装","细分","细胞","细节","终端","终端产品","终端设备","绍兴","经","经济","经济圈","经济效益","经营","经过","经验","经验丰富","结合","结构","结构件","结构设计","给","给排水","绝缘","绝缘材料","绞盘","统筹","统计","继续","绩效","绳锯","维","维修","维护","维生素","综合","综合利用","综合型","综合性","绿亨","绿水青山","绿色","缅甸","编写","编制","缺陷","网","网点","网络","网络安全","网络空间","美","美丽","美国","美好","美好生活","美学","美洲","美的","美菱","美誉度","羚","翰博","翱捷","考核","者","而","耐久","耐材","耐火材料","耗材","耳","职业","职能","联","联动","联合","联合会","联合国","联想","联盟","联网","联美","联迪","聚","聚乳酸","聚合","聚合物","聚焦","聚苯乙烯","聚酯","聚酯树脂","聚酯薄膜","聚集地","肌肉","肌肽","肠道","股东","股份","股份公司","股份制","股本","股票","股票代码","肩负","肺炎","肽","肿瘤","胃","胆碱","背光","背景","胜","脉脉","胰岛素","能","能力","能够","能源","能量","腐蚀","腾远","腾飞","膜","自","自主","自产","自动","自动化","自动控制","自己","自有","自毁","自治区","自然人","自研","自营","自行","自身","至","至今","至佳","致力","致力于","致远","臻","航空器","航空航天","航线","航运","舰船","船东","船舶","船长","船队","良好","良种","色谱","节点","节能","节能产品","节能降耗","芜湖","芝","芬兰","芯片","苏州","苏州市","苏泊尔","英","英业达","英国","英寸","英文","范围","茶叶","荆州市","荣获","荣誉","荣誉称号","药","药业","药企","药品","药品监督管理局","药物","药理","荷兰","莱","莱特","获","获取","获得","获批","获评","菌","萃取","营养","营养食品","营销","著作权","著名","著名商标","董事长","蓝牙","薄膜","虚拟","虚拟现实","蛇毒","蛋","蛋业","蛋制品","蛋白","蜂窝","融入","融合","融资","螺母","螺纹","血液","血清","行业","行业协会","行业标准","行业龙头","行动","行政区","街","衢州市","表现","表面","衬底","袋","被","装备","装置","装配","西安","西汀片","西点","西班牙","西藏","西门子","要求","覆盖","覆盖全国","规划","规格","规模","规模化","规范","规范化","解","解决","解决方案","触头","触媒","计划","计算","计算机软件","计量","订单","认可","认定","认证","让","讯","许可","许可证","论证","设备","设施","设有","设立","设计","证","证书","证券","证券公司","证监局","评为","评价","评估","评定","评审","诊","诊断","诊疗","试制","试剂","试点","试点单位","试验","试验场","试验室","诚","诚信","诚信为本","诚实","该","说明书","诸多","诺思","调度","调试","调配","负极","负责","贡献","贡献奖","财务","财富","责任","责任感","质","质检","质量","质量体系","质量奖","质量方针","质量检验","质量第一","贫血","贯彻","贰级","贴近","贸易","费用","资产","资本","资格","资深","资源","资源管理","资质","资质证书","资金","赋能","赛龙","赞誉","赢","赢得","赣州","赤藓","走","走向","走向世界","走进","起","起来","起草","超","超低温","超净","超声波","超大","超大规模","超导","超导磁体","超硬","超纯","超细粉","超过","超高","越南","越野","越野车","趋势","践行","跟踪","跨国","跨国公司","跨越","跨越式","路","跻身","踏板","身份","车","车削","车程","车载","车辆","车间","轨道交通","转化","转型","转换","转让","轮","轮胎","软","软件","软件产品","软件开发","软硬件","软管","软通","轴承","轻量化","载","载体","载波通信","较","较为","较大","较强","辅助","辅导","辉光","辉煌","辐射","输送","输配电","辰","辰光","边坡","辽宁","辽宁省","达","达到","达泊","迅安","迅速","过","过去","过硬","过程","迎接","运","运作","运动","运用","运维","运营","运营商","运行","运贸","运输","近","近几年","近年来","还","这","这些","进一步","进一步提高","进入","进出口","进口","进口产品","进步","进步奖","进行","远","远洋","远洋运输","远翔","远销","连接","连接器","连续","连锁","迭代","追求","适合","适应","适配","选择","选矿厂","透气","逐年","逐步","逐渐","通","通信","通用","通讯","通过","通道","通风","速率","造","造就","造成","造福","造车","逾","遍及","遍布","遍布全国","道","道路","道钉","遵循","邢台","邦德","郑州","郑州市","部","部件","部分","部门","都","配件","配备","配套","配方","配比","配送","酒","酒店","酰","酶","酶制剂","酸雾","采","采用","采购","采购供应","采集","释放","里","重","重大","重工","重庆","重庆市","重心","重点","重点项目","重视","重组","重要","量产","量化","金","金刚石","金属","金属制造","金融","金融服务","鉴定","鑫","针纺","针织","钢包","钢铁","钣","钨","钴","钻井","钻具","钻头","钻孔","钻石","钾","铁塔","铁氟龙","铁路","铁锂","铜","铜冠","铜合金","铜箔","铜陵","铝塑","铬","铭利达","银行","铸造","链","链条","销售","销售业务","销售收入","销往","销量","锂","锂电池","锂离子","锌粉","镀膜","镇江","镇江市","镍","镍带","镭","长三角","长久","长城汽车","长期","长江","长沙","长沙市","闭环","问题","间","阀门","队伍","防御","防护","防控","防盗器","防盲","防范","阳","阳光","阶段","阿尔斯通","阿里巴巴","降低","降低成本","陕西","院士","院校","除","除了","除垢","陶瓷","随着","隐形","隧洞","雄厚","雅葆轩","集","集中","集团","集团公司","集团化","集团股份","集成","集成化","集成电路","集约化","集群","集装箱","集输","集采","零","零件","零售","零组件","零部件","雷特","雷神","需求","需要","青岛","青岛市","青年","青浦","青睐","非","非常","非常重视","非洲","面向","面对","面料","面板","面积","革新","韩","韩国","顶尖","顶级","项","项目","项目管理","顺应","顾客","颁发","预","预警","预计","预防","领先","领先地位","领先水平","领军","领域","领导","领导者","领跑者","风扇","风景秀丽","风机","风电","风险","飞利浦","飞机","飞行","飞速发展","食品","食品安全","食品工业","食品级","餐饮","饮食","饲料","饲料行业","首","首创","首台","首家","首批","首次","首药","首都","香港","马","驱动","驱动力","驾驶","验证","骏成","骨干企业","高","高低压","高分子","高压","高压电器","高可靠性","高品质","高度","高度重视","高强","高强度","高性能","高技术","高效","高效率","高新","高新产业","高新区","高新技术","高标准","高校","高档","高水平","高温","高科","高科技","高端","高等","高等院校","高精","高精度","高素质","高级","高级职称","高纯","高纯度","高质量","高速","高速铁路","高铁","高附加值","高难度","鲁班奖","鸡蛋","鸿","鹿山","黑龙江","墨西哥","鼓励","齐全","齿轮","龙口","龙头企业","龙门"],"freq":[2,34,3,24,17,4,18,2,23,2,3,2,2,6,5,5,2,4,7,3,2,2,4,2,7,9,9,34,24,9,14,12,10,8,13,8,4,9,17,13,8,4,6,12,10,33,30,20,14,20,28,18,19,2,4,2,7,3,6,2,2,2,4,2,43,2,2,24,9,2,10,3,22,10,5,2,34,11,18,2,3,31,7,4,2,2,3,12,2,5,2,2,22,4,2,3,22,2,2,2,2,5,2,5,3,2,4,4,3,2,2,2,2,2,2,3,3,5,13,3,2,3,6,7,2,5,2,2,2,5,2,2,2,4,2,5,3,12,11,2,3,10,3,8,2,3,5,2,2,3,3,2,2,10,2,4,6,2,11,2,28,4,10,44,3,2,3,2,6,2,2,17,2,9,2,2,2,5,3,6,2,6,2,2,6,4,2,15,2,6,10,2,2,6,2,2,2,2,4,5,2,2,4,2,3,6,4,14,4,3,2,2,4,11,2,9,10,48,18,2,2,2,79,2,12,15,2,2,3,4,2,27,18,5,18,14,2,10,2,3,3,2,2,3,11,2,2,15,2,11,3,11,2,2,14,3,2,14,3,4,2,35,2,3,4,2,3,2,41,2,26,6,33,2,11,4,4,16,3,17,4,2,3,10,2,57,2,6,4,3,5,2,272,111,13,59,7,2,17,2,50,16,2,3,27,4,12,5,5,2,29,6,3,3,5,5,65,3,7,2,4,2,11,4,2,5,6,4,6,2,2,2,2,15,2,2,2,47,3,5,2,81,2,2,179,2,2,4,4,2,3,26,158,6,3,2,2,6,4,6,5,9,2,3,33,19,11,2,462,13,4,5,2,2,2,3,2,3,5,3,3,5,9,16,123,6,5,29,2,4,2,2,3,2,21,351,14,11,3,3,6,2,5,8,275,19,3,7,2,4,20,3,4,3,2,2,3,3,8,4,4,2,2,9,2,4,11,2,2,60,24,3,5,23,505,3,2,5,2,2,7,2,7,26,4,14,2,20,8,5,3,2,17,2,7,6,2,40,6,3,3,2,6,2,2,4,4,5,14,3,3,2,28,2,58,4,5,6,3,3,18,2,6,2,5,197,7,3,17,6,69,26,2,10,14,4,4,2,6,20,9,4,2,9,578,5,3,2,19,3,2,54,13,5,24,3,3,4,33,3,7,4,4,2,2,3,6,2,11,2,7,3,4,50,2,4,2,3,3,7,2,2,55,3,5,3,2,9,2,3,4,9,3,2,2,6,3,9,3,4,38,2,5,2,9,18,2,11,12,34,14,6,21,3,2,6,2,5,2,7,2,4,2,4,2,2,2,6,5,3,2,31,3,8,2,2,2,18,5,25,8,6,3,2,8,4,11,3,2,2,2,2,7,9,12,8,2,56,2,2,5,4,6,6,2,2,3,2,3,7,2,6,2,53,3,3,89,3,3,16,7,10,3,3,2,2,2,5,2,2,3,4,35,3,4,4,62,2,2,8,79,7,2,10,13,2,4,18,2,3,2,2,796,8,2,3,3,3,3,2,3,2,11,4,7,2,2,2,5,5,34,13,2,8,2,17,37,7,3,4,2,30,75,2,3,2,2,25,3,3,2,4,12,2,2,3,9,3,13,7,4,3,6,3,2,5,13,2,3,2,14,3,3,4,2,3,7,2,2,10,3,2,2,3,2,4,2,4,3,2,2,2,2,2,3,3,25,3,4,9,22,3,2,6,9,13,16,4,2,2,3,2,14,3,2,2,9,6,10,13,2,10,12,2,155,17,2,2,12,14,2,22,2,3,2,9,3,30,5,2,5,4,3,26,4,22,3,2,2,2,3,6,3,125,19,3,19,2,12,10,9,7,3,2,2,6,3,6,2,2,2,5,4,13,10,5,2,13,8,2,11,50,3,10,7,4,2,16,3,2,6,2,19,5,2,2,2,65,20,2,2,22,3,2,5,19,6,13,38,3,4,5,2,14,2,7,9,46,11,3,29,5,9,3,5,4,4,2,2,4,6,3,14,5,24,2,4,5,4,2,2,3,2,2,2,2,2,19,2,2,14,3,15,2,63,3,10,3,17,4,2,4,5,7,17,2,13,5,16,6,3,2,4,3,4,2,2,2,2,3,8,3,7,3,4,2,4,6,4,3,4,6,2,2,7,13,4,4,3,28,4,5,3,4,282,18,4,7,2,2,3,5,210,3,8,2,4,4,6,36,3,3,20,3,3,2,6,3,19,2,2,5,2,7,5,2,7,4,4,2,2,2,32,2,5,3,6,2,2,10,4,4,2,13,5,2,15,5,2,2,6,10,34,12,76,20,2,5,5,8,2,6,2,2,10,4,2,2,4,3,3,56,4,5,7,9,6,2,2,8,6,4,9,18,3,2,5,5,40,3,2,694,7,2,6,2,2,2,59,2,2,3,7,14,33,2,4,2,2,11,2,4,7,6,4,2,2,2,3,2,3,5,2,2,5,2,3,2,5,5,2,2,5,3,4,10,10,3,3,2,4,5,55,10,14,2,2,2,2,2,8,4,141,52,3,10,180,3,17,7,5,2,29,3,2,2,3,2,5,4,90,10,2,2,4,2,4,3,308,2,9,2,2,5,22,2,2,8,32,2,6,2,3,5,3,13,3,3,2,3,2,11,29,3,14,3,4,2,68,2,9,2,22,2,24,2,2,9,13,5,2,8,12,4,41,5,3,6,4,45,5,2,8,2,3,4,2,2,2,3,3,2,4,8,6,2,2,12,28,2,2,11,2,3,6,2,3,2,2,2,34,51,4,9,3,3,17,2,56,3,2,4,4,4,7,3,7,52,31,5,2,4,2,2,27,8,2,3,8,3,3,5,2,2,5,3,2,5,2,2,5,2,2,9,5,2,7,3,2,3,3,3,2,4,3,2,2,2,4,3,2,2,3,3,16,6,8,4,3,7,6,8,2,2,3,33,3,2,3,2,10,8,3,5,3,7,41,3,2,2,2,4,2,2,2,2,8,4,6,6,3,3,3,90,2,3,2,6,4,7,8,3,39,7,12,12,7,2,5,2,8,15,2,2,5,21,24,5,58,20,6,5,4,8,34,2,15,2,6,5,2,3,219,4,4,2,2,28,2,2,6,4,2,9,2,2,2,2,2,3,2,24,2,3,3,2,2,3,3,17,2,2,2,9,65,6,27,3,3,3,2,3,3,7,4,3,2,4,4,6,2,2,3,3,2,5,4,10,2,3,3,10,17,2,2,2,3,2,13,7,45,3,6,3,4,24,27,9,7,11,3,4,50,2,6,8,25,2,10,2,36,2,2,2,25,2,2,2,9,98,4,19,4,3,2,4,4,2,100,5,10,4,2,4,3,7,2,25,6,2,2,2,3,3,2,7,3,5,3,5,2,50,16,11,6,2,333,7,4,2,7,16,3,2,2,140,8,6,2,2,2,13,55,3,4,12,12,26,28,2,4,2,3,4,90,14,4,2,6,3,7,4,3,5,2,7,2,10,20,4,80,10,9,47,2,2,3,2,3,94,18,4,3,5,14,9,7,2,3,3,10,2,2,15,15,2,2,39,2,6,2,12,3,2,3,2,2,51,3,3,11,15,7,11,9,3,5,2,11,4,15,3,4,2,2,2,4,19,2,3,2,3,4,15,12,4,4,25,2,2,3,3,4,6,2,2,3,4,5,2,3,5,2,7,3,4,9,2,4,10,100,42,7,3,8,7,3,8,7,8,3,113,2,19,5,15,2,5,56,6,17,28,48,4,2,4,20,3,2,2,11,3,7,4,8,2,3,2,45,2,2,4,8,2,6,3,2,3,7,4,3,6,23,2,7,2,369,7,39,4,10,5,7,4,4,2,2,7,3,2,2,3,8,2,20,26,3,3,8,2,5,3,2,2,5,4,14,12,2,4,189,4,2,72,6,39,4,2,2,2,3,3,5,11,3,4,3,7,11,20,15,4,2,2,3,3,6,2,2,5,39,2,9,2,19,4,14,9,2,4,2,22,2,2,160,9,4,47,2,20,2,5,8,2,3,2,5,2,2,6,3,13,4,2,2,3,5,2,9,9,2,2,5,4,5,2,2,6,9,4,4,2,6,3,2,2,6,6,4,2,2,2,2,22,16,21,4,3,2,2,2,15,2,2,2,4,18,7,2,4,2,2,6,2,21,10,2,138,7,5,3,3,2,3,2,7,2,4,2,7,35,3,10,4,6,14,3,8,7,5,28,2,11,6,7,3,2,4,3,2,2,45,2,14,2,2,2,5,10,7,3,2,3,2,4,2,2,3,267,26,9,3,2,2,3,3,3,6,37,73,15,6,5,2,3,33,2,2,6,6,2,5,8,107,2,45,2,2,13,7,2,3,4,262,5,2,252,6,6,11,2,4,3,3,3,4,3,2,6,2,7,4,2,3,3,2,2,31,4,3,4,9,4,5,2,3,2,7,3,15,3,16,2,2,3,3,2,5,4,3,2,140,4,17,6,2,3,2,2,17,3,2,6,3,2,5,9,18,3,3,6,4,2,3,9,47,20,4,2,8,2,3,2,6,2,4,3,84,2,25,9,5,12,5,3,2,3,2,2,3,2,2,2,81,2,23,3,2,2,2,10,9,6,3,2,3,25,6,18,2,3,5,2,5,3,5,14,11,8,6,8,6,22,3,7,5,11,4,2,2,4,2,5,8,3,3,3,3,2,2,5,8,8,3,6,8,3,8,2,3,7,6,3,5,2,5,2,29,2,2,2,2,2,2,2,2,3,24,34,5,6,2,3,3,2,2,2,5,2,83,4,3,5,6,3,4,7,8,19,2,3,2,6,13,3,4,2,2,2,3,2,18,11,2,11,2,4,2,5,3,18,2,2,8,4,4,2,2,3,2,2,6,2,2,2,2,13,14,45,7,6,3,29,2,35,2,2,3,2,2,2,8,3,5,2,2,2,2,2,2,2,2,2,2,14,3,5,2,11,4,2,4,2,5,2,13,4,7,3,8,3,16,12,3,11,13,2,8,8,5,2,7,12,2,2,2,3,15,9,7,2,15,3,23,7,3,2,2,4,4,7,3,5,2,6,3,2,2,2,2,5,2,6,2,2,2,2,6,12,2,2,6,3,4,2,2,2,19,3,2,2,2,5,2,5,3,3,2,3,2,4,2,25,2,9,4,2,7,4,3,2,27,4,5,15,2,10,2,5,8,3,2,4,2,2,2,37,3,42,2,4,4,4,5,14,18,3,4,2,16,17,8,2,2,6,2,3,3,3,2,2,3,69,2,2,2,3,2,2,2,303,6,10,35,11,6,2,3,3,6,2,16,38,3,2,4,2,39,14,32,4,2,7,2,19,2,2,2,9,11,3,20,2,5,7,2,2,7,5,73,4,5,2,2,3,2,4,2,2,5,3,10,28,15,4,2,2,7,11,4,2,4,3,3,2,3,8,2,4,2,2,7,4,2,2,4,2,2,2,8,3,1968,2,2,2,4,7,18,3,4,2,84,5,19,10,2,5,37,3,2,5,2,18,2,2,4,38,3,9,2,5,7,12,2,4,9,4,2,2,34,9,14,10,3,33,2,8,3,12,3,2,2,4,5,2,2,2,7,4,4,5,9,335,70,2,7,3,22,7,5,3,4,5,3,7,6,2,5,11,10,2,3,9,2,14,3,2,2,2,2,33,30,3,4,5,2,2,2,8,17,4,2,2,3,38,3,2,4,7,3,8,14,4,2,15,125,3,2,10,11,77,11,5,4,27,3,3,2,5,11,29,3,39,19,2,24,2,7,19,6,2,3,2,2,6,3,4,4,2,2,8,2,9,2,2,2,2,2,2,10,4,3,15,27,2,2,2,3,2,5,9,7,4,2,2,2,6,6,2,2,513,5,2,4,2,35,5,5,4,2,2,6,112,88,2,2,2,2,2,7,2,6,5,7,2,24,2,2,4,5,3,4,2,2,3,2,2,5,5,48,2,2,2,2,6,3,5,2,4,3,4,2,2,4,4,7,53,21,72,2,2,3,2,6,10,3,4,6,5,2,2,6,23,2,3,8,4,6,16,8,2,4,4,7,2,5,4,2,18,11,2,18,3,6,14,3,2,26,4,2,4,11,42,3,2,66,41,33,9,18,12,12,2,8,2,4,5,4,2,4,7,2,2,2,3,3,6,46,2,2,5,5,2,15,2,2,5,2,8,2,30,8,2,9,2,39,6,3,2,4,3,7,3,2,5,3,2,3,9,2,3,4,4,2,17,2,3,3,21,3,2,3,5,30,2,5,5,8,2,2,12,10,2,4,3,2,2,2,3,6,153,2,6,2,7,32,2,2,3,2,2,2,9,7,2,2,2,14,70,8,25,2,2,5,2,17,31,78,2,13,18,3,5,6,2,5,2,2,6,3,12,10,6,2,5,76,3,5,2,6,2,4,3,3,7,2,3,31,2,4,2,12,2,2,4,2,2,43,14,3,2,2,2,5,4,2,10,3,2,31,23,13,16,5,2,9,3,13,2,2,2,5,10,3,76,4,5,4,5,9,3,25,10,12,11,2,2,2,4,3,3,4,3,6,2,3,2,22,4,2,2,2,4,169,4,19,2,3,4,2,2,3,6,8,2,68,33,8,3,8,2,3,2,3,4,19,23,4,9,4,29,11,16,5,2,3,75,7,9,22,2,3,7,2,22,35,154,21,6,2,8,3,110,8,15,29,104,2,17,29,5,2,24,2,3,2,2,2,2,3,3,5,7,4,15,11,6,3,20,6,3,6,2,7,2,2,3,2,3,6,11,6,2,4,10,2,2,2,113,12,5,7,2,6,2,3,2,4,4,2,11,9,2,5,15,2,11,2,2,5,4,3,8,14,4,3,10,2,2,2,12,3,11,13,2,2,3,2,2,5,2,8,2,2,20,3,2,6,2,2,6,2,2,2,2,2,8,2,2,3,6,2,2,3,2,17,7,15,19,4,12,3,2,5,30,6,5,4,6,5,17,2,2,4,2,28,8,5,12,5,2,2,3,5,5,3,3,8,2,2,2,7,21,2,4,4,5,3,6,17,2,2,4,7,7,8,38,6,6,2,9,8,2,10,18,3,2,15,2,24,7,9,2,13,8,20,2,3,2,2,14,4,5,13,6,4,19,2,3,2,4,2,5,2,12,5,5,41,7,6,131,3,4,2,5,3,2,2,2,5,7,6,3,4,6,3,7,2,3,6,4,10,7,7,3,13,4,5,25,3,2,2,2,2,2,5,2,3,2,22,10,2,5,3,8,11,23,3,7,5,3,57,4,9,2,22,5,3,5,23,15,2,5,2,3,3,2,5,4,3,2,2,7,2,10,3,3,4,4,5,2,9,2,7,3,4,9,2,5,3,4,4,7,4,3,118,6,3,4,2,7,2,8,2,4,2,2,2,4,5,6,2,2,21,2,2,2,2,3,3,7,10,4,4,4,2,3,2,3,2,5,2,2,2,2,3,8,5,2,2,2,8,7,5,2,6,7,35,4,39,4,4,9,9,2,21,2,4,4,3,2,2,3,6,8,23,5,4,44,2,14,5,2,2,4,5,2,2,6,11,2,2,6,7,4,5,3,2,3,98,68,2,2,14,18,2,3,2,2,52,5,5,18,170,2,3,2,2,3,5,2,3,3,5,2,2,32,11,3,2,3,2,12,2,2,6,2,4,10,3,4,3,4,3,14,3,3,4,4,4,40,2,9,11,2,4,18,8,3,3,2,16,5,25,3,10,2,5,129,4,13,7,7,6,3,11,34,3,2,2,8,6,9,2,13,3,12,6,3,7,2,3,2,2,4,2,4,2,3,5,7,5,16,2],"fontFamily":"Segoe UI","fontWeight":"bold","color":"random-dark","minSize":0,"weightFactor":0.09146341463414634,"backgroundColor":"white","gridSize":0,"minRotation":-0.7853981633974483,"maxRotation":0.7853981633974483,"shuffle":true,"rotateRatio":0.4,"shape":"circle","ellipticity":0.65,"figBase64":null,"hover":null},"evals":[],"jsHooks":{"render":[{"code":"function(el,x){\n console.log(123);\n if(!iii){\n window.location.reload();\n iii = False;\n\n }\n }","data":null}]}}</script> --- Claudia Goldin 发表刊物标题词云 <img src="Goldin.png" width="1147" />